Question 1195204: Solve these two equations:
(a) The quadratic equation  has two roots. If one root is five times the other, what is the value of a? has two roots. If one root is five times the other, what is the value of a?
(b) If  and and  are factors of the polynomial are factors of the polynomial  , find , find  . .
Found 3 solutions by ikleyn, lotusjayden, MathTherapy:
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve these two equations:
(a) The quadratic equation  has two roots. has two roots.
If one root is five times the other, what is the value of a?
(b) If  and and  are factors of the polynomial are factors of the polynomial  , ,
find  . .
~~~~~~~~~~~~~~~~~~
Part (a)
Let z be one root of the equation; then 5z is another root.
Apply the Vieta's theorem. it gives you these two equations for unknowns "a" and "z":
(1) the sum of the roots z and 5z is equal to 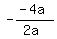 = 2
z + 5z = 2, or 6z = 2, z = = 2
z + 5z = 2, or 6z = 2, z = 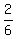 = =  .
(2) the product of the roots is equal to .
(2) the product of the roots is equal to 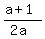 z*(5z) =
z*(5z) = 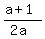 , which implies , which implies 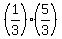 = = 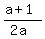 , ,
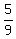 = = 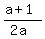 , 5*(2a) = 9*(a+1), 10a = 9a + 9, a = 9.
Thus we get the ANSWER : a = 9. , 5*(2a) = 9*(a+1), 10a = 9a + 9, a = 9.
Thus we get the ANSWER : a = 9.
Part (a) is solved.
///////////////
Two problems in your post are different.
At this forum, I do not recommend to pack more than one problem to post, in order for do not create a MESS.
Therefore, post your second problem separately, and I will show you how to solve it.
By the way, the rules of this forum PROHIBIT posting more than one problem at once.
The rules are at this web-page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
Answer by lotusjayden(18)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
|
|
|