You can
put this solution on YOUR website! .
Find the least integer by which 8100 must be multiplied to obtain a perfect cube
~~~~~~~~~~~~~~~~~~~~
8100 = 81*100 = 9^2*10^2 = 2^2*3^4*5^2.
To make a perfect cube, we should have indexes at prime factors multiple of 3.
From here, it is clear that the least such integer number to multiply is 2*3^2*5 = 9*10 = 90.
Then the product is 8100*90 = 729000.
CHECK. 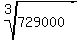 = 90.
ANSWER. The least integer by which 8100 must be multiplied to obtain a perfect cube is 90.
= 90.
ANSWER. The least integer by which 8100 must be multiplied to obtain a perfect cube is 90.
Solved and explained.