SOLUTION: For which values of k do the lines {{{x+ky=4}}} and {{{2x-3y=6}}} intersect in the 3rd quadrant? Write your answer as an open interval.

To be in the 3rd quadrant, the intersection point must have both coordinates,
x and y, negative.


So, let start with the given system of equations

     x + ky = 4    (1)
  
    2x - 3y = 6    (2)


Multiply first equation by 2.  You will get an equivalent system

    2x + 2ky = 8   (3)

    2x -  3y = 6   (4)    <<<---=== same as (2)


Subtract eq(4) from eq(3).  You will get

    (2k+3)y = 2,  or  y = 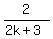.   (3)


In order for 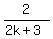  be negative, the condition  

    2k + 3 < 0    (5)

should be satisfied,  or  

    k < .


Next, with the found value of y in (3), we can find x from equation (1)

    x = 4 - ky = 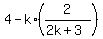 =  =  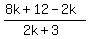= 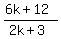.   (6)


Above, we just found that (2k+3) must be negative.

HENCE, in order for x be negative, the numerator in (6) must be positive: 

    6k + 12 > 0,

or 

    6(k+2) > 0,

which means that  

    k +2 > 0,  

or

    k > -2.


Thus the condition on k, which provides the intersection point in the 3rd quarter, is

    -2 < k < ,

or, in the interval form, k must be in the open interval (-2,-1.5).