Question 1195176: You roll two six-sided fair dice.
a. Let A be the event that either a 3 or 4 is rolled first followed by an odd number.
P(A) =
Round your answer to four decimal places.
b. Let B be the event that the sum of the two dice is at most 7.
P(B) =
Round your answer to four decimal places.
c. Are A and B mutually exclusive events?
d. Are A and B independent events?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
One and ONLY ONE problem/question per post.
It is the RULE, the POLICY and the REQUIREMENT of this forum.
It is written in this page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
\\\\\\\\\\\\\\\\\\\\\\
One question is fine.
Two questions for one problem is still admittable.
But 4 (four) questions in one post is FAR BEYOND the BOUNDS
that a reasonable person in healthy mind may allow to himself.
////////////////////////////////////////////////////////////////
Below is my addition, which I made after reading the post by @greenestamps.
In the post by @greenestamps, the reasoning, related to question (d), is INCORRECT, and his answer is WRONG.
It requires more accurate analysis, which is presented below.
To determine, if events A and B are independent, you should check if P(A ∩ B) = P(A)*P(B).
+-------------------------------------------------------------------+
| If the equality is valid, the events are independent; |
| if the equality is not valid, the events are not independent. |
+-------------------------------------------------------------------+
Event A has the following 6 outcomes :
(3,1), (3,3), (3,5), (4,1), (4,3), (4,5).
Therefore, the probability P(A) is  =  .
Event B has 21 outcomes. Therefore, the probability P(B) =  =  .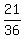
Event (A ∩ B) has the following 4 outcomes : (3,1), (3,3), (4,1), (4,3).
Therefore, P(A ∩ B) is  =  .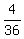
But P(A)*P(B) = 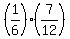 =  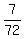is not equal to P(A ∩ B) = .
It shows/proves that the events A and B are not independent.
ANSWER to question (d): the events A and B are not independent.
Solved.
-------------------
Two lessons to learn from my post :
(1) If you put many questions in your post, the probability is high that you will get a MESS in response.
(2) @greenestamps calls my right response as idiotic, but sells you his wrong response as correct.
From it, make your own conclusions.
/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
Wow, @greenestamps, how much expression in your last invectives (!)
One can immediately see an educated intelligent person, even from afar.
Your vocabulary is much wider than my - I even don't know such English words (!)
Perhaps, I will not answer you - it will be better that way.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Sorry you have to put up with the idiotic responses from some tutors on this site....
Your SINGLE problem contains four questions, all of which are interrelated; the post HAS TO contain all four questions. It would be absurd to post the 4 questions in your post separately!
a. P(3 or 4) on first roll = 2/6 = 1/3
P(odd on second roll = 3/6 = 1/2
P((3 or 4 on first) AND (odd on second)) = (1/3)(1/2) = 1/6
b. P(sum at most 7) = P(2)+P(3)+P(4)+P(5)+P(6)+P(7) = (1/36)+(2/36)+(3/36)+(4/36)+(5/36)+(6/36) = 21/36 = 7/12
c. The events are not mutually exclusive -- it is possible to get a 3 or 4 on the first roll and get a sum of at most 7 on the two rolls.
d. The events are independent. The probability of getting a sum of at most 7 on the two dice is not affected by the probability of getting a 3 or 4 on the first roll; and vice versa.
---------------------------------------------------------------------
Dear idiot tutor @ikleyn --
Your answer was NOT right; you didn't even answer the question!!!
And it WAS idiotic to say that the original post shouldn't have included four different questions, because they were all part of one problem.
When, oh when, will you learn not to be such an arrogant pain in the butt?
|
|
|
