Question 1195173: A factory received a shipment of 33 sprockets, and the vendor who sold the items knows there are 7 sprockets in the shipment that are defective. Before the receiving foreman accepts the delivery, he samples the shipment, and if too many of the sprockets in the sample are defective, he will refuse the shipment.
If a sample of 7 sprockets is selected, find the probability that none in the sample are defective.
Answer by ikleyn(52809)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A factory received a shipment of 33 sprockets, and the vendor who sold the items knows there are 7 sprockets
in the shipment that are defective. Before the receiving foreman accepts the delivery, he samples the shipment,
and if too many of the sprockets in the sample are defective, he will refuse the shipment.
If a sample of 7 sprockets is selected, find the probability that none in the sample are defective.
~~~~~~~~~~~~~~~~~~~~
So, there are 7 bad sprockets and 33-7 = 26 good sprockets in the 33 sprockets shipment.
The probability that 1-st selected sprockets is good is 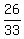 .
The probability that 2-nd selected sprockets is good is .
The probability that 2-nd selected sprockets is good is 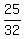 .
The probability . . . and so on . . .
Thus the final probability is the product of 7 fractions
P = .
The probability . . . and so on . . .
Thus the final probability is the product of 7 fractions
P =  = 0.153978. ANSWER = 0.153978. ANSWER
Solved.
The other way to solve is this reasoning.
In all, there are 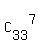 = 4272048 different ways to select 7 items from 33 items.
If all selected items are good, it means that we select them from the subset of 26 good items.
There are = 4272048 different ways to select 7 items from 33 items.
If all selected items are good, it means that we select them from the subset of 26 good items.
There are 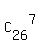 = 657800 different ways to select 7 items from 26 items.
So, the probability under the problem's question is = 657800 different ways to select 7 items from 26 items.
So, the probability under the problem's question is  = 0.153978, giving the same answer. = 0.153978, giving the same answer.
Solved.
You may use any of the two presented ways to solve the problem.
|
|
|