SOLUTION: The Phone-A-Way company offers two different monthly cell phone plus. Plan X costs $0.25 for each minute of talk-time. Plan Y costs $9.75 for up to 150 minutes of talk-time and $0.

Consider coordinate plane (minutes, dollars), where minutes are horizontal coordinate axis;
vertical coordinate line is for dollars.


Plan X graphically is the sloped straight line through the origin of the coordinate system
(minutes,dollars) with the slope of 0.25 dollars per minute.


Plan Y is the horizontal line Y = 9.75 from  m= 0 minute  to m= 150 minutes inclusive;
then after m > 150 minutes it is the straight line with the slope 0.5 dollars per minute.


    +--------------------------------------------------------+
    |    Make a sketch in accordance with this description.  |
    |    From the sketch, notice that line X                 |
    |    intersects line Y at two pints.                     |
    +--------------------------------------------------------+


First intersection point is when  0.25m = 9.75 dollars;  it is at  m = 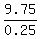 = 39 minutes.


Since we consider m > 40 (see the condition), this intersection point is out of our interest.


Next intersection point is when  0.25m = 9.75 + 0.5*(m-150).


Find m from this equation, simplifying it step by step

    0.25m = 9.75 + 0.5m - 0.5*150

    0.25m - 0.5m = 9.75 - 0.5*150

        - 0.25m  =    -65.25

              m  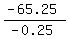=     = 261 minutes.


It is your ANSWER: the value of m satisfying to imposed conditions is 261 minutes.


CHECK.  At m= 261, plan X costs  261*0.25 = 65.25 dollars.

        At t = 261, plan Y costs 9.75 + 0.5*(261-150) = 65.25 dollars, i.e. the same amount,

                    which shows that the solution and the answer are correct.