Question 1195138: A bag contains red, white, green, and blue marbles. There are an equal number of red marbles and white marbles, and fice times as many green marbles as blue marbles. There is a 35% chance of selecting a red marble first. What is the fewest possible number of green marbles in the bag?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52800)   (Show Source):
You can put this solution on YOUR website! .
A bag contains red, white, green, and blue marbles.
There are an equal number of red marbles and white marbles,
and  five times as many green marbles as blue marbles.
There is a 35% chance of selecting a red marble first.
What is the fewest possible number of green marbles in the bag?
~~~~~~~~~~~~~~~
Let the number of blue marbles be x.
Then the number of green marbles is 5x.
Since there is a 35% chance of selecting a red marble first,
it means that the number of red marbles is 0.35 of the total number of marbles.
Since there are an equal number of red marbles and white marbles,
it means that the number of white marbles is 0.35 of the total number of marbles, too.
Thus we have red + white = 0.7 of total number of marbles;
hence, green + blue marbles = the rest 0.3 of the total number of marbles = 5x + x = 6x.
Thus 0.3 of the total marbles is the number multiple of 6;
hence, the minimum total number of marbles is 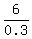 = 20 or multiple to it.
+----------------------------------------------------------------+
| Now we check if this found total number of 20 marbles |
| does really work. |
+----------------------------------------------------------------+
If the total number of marbles is 20, then the number of red + white is 0.7*20 = 14;
hence, the number of red marbles = number of white marbles = 7.
Then the rest 20-14 = 6 marbles are blue + green,
and from it, we easily conclude that there is 1 blue marble and 5 green marbles.
Thus this reasoning gives the ANSWER : fewest possible number of green marbles in the bag is 5.
Solved.
-------------------
Thanks for posting this problem.
It is really good mental exercise for a brain.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The probability is 35% that a red marble is selected first, and the numbers of red and white marbles are the same, so the probability is also 35% that a white marble is selected first.
That means the probability of selecting either a blue or green marble first is (100-35-35) = 30%.
Then, since the number of green marbles is 5 times the number of blue marbles, that 30% probability of selecting either a blue or a green breaks down into a 25% probability of selecting a green and a 5% probability of selecting a blue.
The ratio of the numbers of marbles of the different colors is the same as the ratio of the probabilities of selecting each color first: B:G:R:W = 5:25:35:35 = 1:5:7:7.
So the smallest possible number of green marbles in the bag is 5.
ANSWER: 5
|
|
|
