Question 1195112: Sid wants to find the height of a tree without having to climb it, but it is a cloudy day, so he cannot use
shadows. He takes a mirror from his pocket and places it on the ground 7.2 m from the base of the
tree. He backs up until he can see the top of the tree in the mirror, a distance of 1.2 m from the mirror.
If Sid's eyes are 1.5 m above the ground, what is the height of the tree?
Answer by ikleyn(52818)   (Show Source):
You can put this solution on YOUR website! .
Sid wants to find the height of a tree without having to climb it, but it is a cloudy day,
so he cannot use shadows. He takes a mirror from his pocket and places it on the ground
7.2 m from the base of the tree. He backs up until he can see the top of the tree in the mirror,
a distance of 1.2 m from the mirror.
If Sid's eyes are 1.5 m above the ground, what is the height of the tree?
~~~~~~~~~~~~~~~~~
Solution
In the Figure below, AB represents the tree; CD represents Sid and ==== represents the mirror.
The rays of light are shown by points.
According to the optics law (the reflection law), angle AMB is equal to angle CMD,
so the right-angled triangles AMB and CMD are similar.
From the triangles similarity, we have this proportion  =  .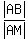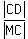
Substituting the given values there, we have 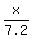 =  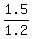, where x is the height of the tree.
It gives the solution for the tree's height x =  = 6*1.5 = 9 meters.
ANSWER. The height of the tree is 9 meters.
Solved.
B
+
/|\ .
/ | \ .
/ /|\ \ . D
/ | \ . o
/ /|\ \ . . _|_
/ | \ . . / | \
| . . |
+---------------------=====------/ \--
A M C
F i g u r e
|
|
|
