SOLUTION: The lengths indicated on the rectangle shown are in centimeters. What is the number of square centimeters in the area of the shaded region?

The given BIGGEST rectangle has dimensions 2+6 = 8 units by 9+5 = 14 units.

If the left lover corner of this rectangle is (0,0), the origin, then OBVIOUSLY, 
the center point of the rectangle is (7,4).


The area of the big rectangle is 8*14 square units, and 1/4 of its area is 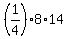 = 28 square units.

    OK.  Let's consider the shaded quadrilateral.


Then it is OBVIOS that the area of the shaded quadrilateral is equal to 1/4 of the area 
of the BIG rectangle plus the area of the adjacent "vertical" right-angled triangle 
minus the area of the adjacent "horizontal" right angled triangle.   (*)


Adjacent "vertical" triangle has the legs 8-4 = 4 units (vertical) and 9-7 = 2 units (horizontal);
so its area is  (1/2)*4*2 = 4 square units.


Adjacent "horizontal" triangle has the legs 8-4-2 = 2 units (vertical) and 14-7 = 7 units (horizontal);
so its area is  (1/2)*2*7 = 7 square units.


Therefore, the area of the shaded region, according to the wording formula (*) is

    28 + 4 - 7 = 25 square units.    ANSWER

    (1)  take one fourth of the area of the big rectangle;

    (2)  add the area of the adjacent "vertical" right-angled triangle;

    (3)  subtract the area of the adjacent "horizontal" right-angled triangle.