Question 1194945: Please help me solve this word problem about Compound Events:(union, intersection and complement):
Of 500 college students, 115 are enrolled in math, 205 are enrolled in English, and 45 are enrolled in both. If a student is selected at random, find the probability of the following. (See Example 5. Round your answers to three decimal places.)
(a) The student is enrolled in mathematics.
(b) The student is enrolled in English.
(c) The student is enrolled in both.
(d) The student is enrolled in mathematics or English.
(e) The student is enrolled in English but not in mathematics.
(f) The student is not enrolled in English or is enrolled in mathematics.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
M = event of selecting a student in math
P(M) = probability of selecting a math student
P(M) = (number of math students)/(number total)
P(M) = 115/500
P(M) = 0.23
Answer: 0.23
===========================================================
Part (b)
E = event of selecting a student in English
P(E) = probability of selecting an English student
P(E) = (number of English students)/(number total)
P(E) = 205/500
P(E) = 0.41
Answer: 0.41
===========================================================
Part (c)
E and M = event of selecting student in both classes
P(E and M) = (number in both)/(number total)
P(E and M) = 45/500
P(E and M) = 0.09
Answer: 0.09
===========================================================
Part (d)
E or M = event of selecting a student in either class (or both)
n(E or M) = number of students in either class or both
n(E or M) = n(E) + n(M) - n(E and M)
n(E or M) = 205 + 115 - 45
n(E or M) = 275
P(E or M) = n(E or M)/(number total)
P(E or M) = 275/500
P(E or M) = 0.55
Answer: 0.55
===========================================================
Part (e)
n(E) = number in English class = 205
n(E and M) = number in both classes = 45
n(E not M) = number in English, but not math
n(E not M) = n(E) - n(E and M)
n(E not M) = 205 - 45
n(E not M) = 160
P(E not M) = n(E not M)/(500 total)
P(E not M) = 160/500
P(E not M) = 0.32
Answer: 0.32
===========================================================
Part (f)
I interpret this to mean "find the probability of someone that isn't in either class". Let me know if your teacher meant something else.
500 total students
n(E or M) = 275 in either class
n(not E and not M) = 500 - n(E or M)
n(not E and not M) = 500 - 275
n(not E and not M) = 225 students in neither class
225/500 = 0.45 is the probability of selecting a student that is not in English, and also not in Math either.
Answer: 0.45
Answer by ikleyn(52782)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help me solve this word problem about Compound Events:(union, intersection and complement):
Of 500 college students, 115 are enrolled in math, 205 are enrolled in English, and 45 are enrolled in both.
If a student is selected at random, find the probability of the following.
(See Example 5. Round your answers to three decimal places.)
(a) The student is enrolled in mathematics.
(b) The student is enrolled in English.
(c) The student is enrolled in both.
(d) The student is enrolled in mathematics or English.
(e) The student is enrolled in English but not in mathematics.
(f) The student is not enrolled in English or is enrolled in mathematics.
~~~~~~~~~~~~~~~~
(a) P(M) = 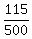 .
First, it is obvious and does not require further explanation.
I intently left it without reducing the fraction, to make logic and expression clear to you.
You may reduce it on your own.
(b) P(E) = .
First, it is obvious and does not require further explanation.
I intently left it without reducing the fraction, to make logic and expression clear to you.
You may reduce it on your own.
(b) P(E) = 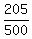 .
Again, it is obvious and does not require further explanation.
I intently left it without reducing the fraction, to make logic and expression clear to you.
You may reduce it on your own.
(c) P(M and E) = .
Again, it is obvious and does not require further explanation.
I intently left it without reducing the fraction, to make logic and expression clear to you.
You may reduce it on your own.
(c) P(M and E) = 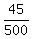 .
Again, it is obvious, because it is given that 45 students are enrolled in both.
I intently left it without reducing the fraction, to make logic and expression clear to you.
You may reduce it on your own.
(d) P(M or E) = use the formula for the UNION of events, which is = P(M) + P(E) - P(M and E).
Each of the three terms in the right side is just calculated above in (a), (b) and (c). So you simply
substitute the relevant values in this formula
P(M or E) = P(M) + P(E) - P(M and E) = .
Again, it is obvious, because it is given that 45 students are enrolled in both.
I intently left it without reducing the fraction, to make logic and expression clear to you.
You may reduce it on your own.
(d) P(M or E) = use the formula for the UNION of events, which is = P(M) + P(E) - P(M and E).
Each of the three terms in the right side is just calculated above in (a), (b) and (c). So you simply
substitute the relevant values in this formula
P(M or E) = P(M) + P(E) - P(M and E) = 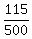 + + 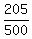 - - 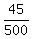 .
Calculate and then reduce the fraction on your own.
(e) P(E but not M) = P(E) - P(M and E).
Simply from P(E) subtract P(M and E).
Wording explanation is that you want that part of E which is not (M and E).
Again, you just know P(E) from (b) and know P(M and E) from (c),
so all you need is to substitute those values into the formula
P(E but not M) = P(E) - P(M and E) = .
Calculate and then reduce the fraction on your own.
(e) P(E but not M) = P(E) - P(M and E).
Simply from P(E) subtract P(M and E).
Wording explanation is that you want that part of E which is not (M and E).
Again, you just know P(E) from (b) and know P(M and E) from (c),
so all you need is to substitute those values into the formula
P(E but not M) = P(E) - P(M and E) = 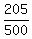 - - 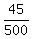 .
Calculate and then reduce the fraction on your own.
(f) Regarding (f), it is too MUCH questions for one post,
so and THEREFORE I do not go into further explanations. .
Calculate and then reduce the fraction on your own.
(f) Regarding (f), it is too MUCH questions for one post,
so and THEREFORE I do not go into further explanations.
My rule is DO NOT PACK too much in one post, since otherwise the student's brain does not process it.
It requires and deserves a SEPARATE post.
At this point, I complete my explanations.
Please let me know if you do understand everything and every point from the outlined explanations.
////////////////
To see many other similar (and different) solved problems, look into the lessons
- Elementary operations on sets help solving Probability problems
- Elementary operations on sets help solving Probability problems - REVISITED
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Solved problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Consider these lessons as your textbook, handbook, a Solutions Manual, tutorials and (free of charge) home teacher.
Happy learning (!)
|
|
|