Question 1194941: In choosing what music to play at a charity fund raising event, Cory needs to have an equal number of symphonies from Haydn, Mendelssohn, and Mahler. If he is setting up a schedule of the 12 symphonies to be played, and he has 104 Haydn, 17 Mendelssohn, and 9 Mahler symphonies from which to choose, how many different schedules are possible? Express your answer in scientific notation rounding to the hundredths place.
Answer by ikleyn(52792)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In choosing what music to play at a charity fund raising event,
Cory needs to have an equal number of symphonies from Haydn, Mendelssohn, and Mahler.
If he is setting up a schedule of the 12 symphonies to be played,
and he has 104 Haydn, 17 Mendelssohn, and 9 Mahler symphonies from which to choose,
how many different schedules are possible?
Express your answer in scientific notation rounding to the hundredths place.
~~~~~~~~~~~~~~~~
Cory can choose 4 symphonies from 104 symphonies by Haydn in 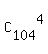 = 4598126 different ways.
Cory can choose 4 symphonies from 17 symphonies by Mendelssohn in = 4598126 different ways.
Cory can choose 4 symphonies from 17 symphonies by Mendelssohn in  = 2380 different ways.
Cory can choose 4 symphonies from 9 symphonies by Mahler in = 2380 different ways.
Cory can choose 4 symphonies from 9 symphonies by Mahler in 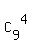 = 126 different ways.
So, Cory can combine = 126 different ways.
So, Cory can combine 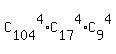 = 4598126 * 2380 * 126 = 1378886024880
different sets of 12 symphonies taking 4 symphonies of each of the three famous composers.
+-----------------------------------------------------------------------+
| But this number is not yet the number of all possible schedules. |
+-----------------------------------------------------------------------+
To get the number of all possible schedules, we should take every of these 1378886024880 sets
and make it a subject of all possible 12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479001600 permutations.
After this permutization of each of 1378886024880 sets, we get the total number of all possible schedules = 4598126 * 2380 * 126 = 1378886024880
different sets of 12 symphonies taking 4 symphonies of each of the three famous composers.
+-----------------------------------------------------------------------+
| But this number is not yet the number of all possible schedules. |
+-----------------------------------------------------------------------+
To get the number of all possible schedules, we should take every of these 1378886024880 sets
and make it a subject of all possible 12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479001600 permutations.
After this permutization of each of 1378886024880 sets, we get the total number of all possible schedules
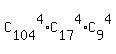 * 12! = 1378886024880 * 479001600 = * 12! = 1378886024880 * 479001600 = 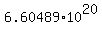 schedules.
You can round this number to the requested form and get the ANSWER : there are schedules.
You can round this number to the requested form and get the ANSWER : there are 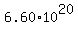 different possible schedules. different possible schedules.
Solved.
|
|
|