Question 1194920: 1. If p, q, r are three points of a line and the coordinates of p and r are √3 and -√18, what is the coordinate of q given that pq = qr.
2. p, q, and r are three points of a line with coordinates x, y, and z in that order. If |x - z| + |z- y| = |x-y|, which point lies between the other two? Explain your answer
3. If p,q, and r are three points on a circle, can you identify which point is between the other two? Discuss.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
I will answer question 1, ONLY.
The problem hesitates to say that p, q and r are the points on a  line;
so, they are not simply the points on the line.
As elements of a number line, they are the NUMBERS.
p =  , r = 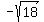 and pq = qr.
From pq = qr we have pq = rq, pq - rq = 0, (p-r)q = 0.
Since p =/= r, the factor in parentheses, (p-r), is different from zero.
THEREFORE, (p-r)q = 0 implies q= 0.
ANSWER. From the given conditions, we derived that q = 0.
Solved.
/////////////
I do not touch questions 2 and 3, because everything is OBVIOUS there.
\\\\\\\\\\\\
A special note to the person who created this problem.
Math problem should not hesitate to tell a truth.
Otherwise, it is not a Math problem.
Or a bad style to present a Math problem.
|
|
|
