SOLUTION: Please help me solve this question:log2{√(x³-2x²+x)}=1+log2(x-1)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Please help me solve this question:log2{√(x³-2x²+x)}=1+log2(x-1)      Log On


   

Question 1194878: Please help me solve this question:log2{√(x³-2x²+x)}=1+log2(x-1)
Found 3 solutions by greenestamps, MathTherapy, MathLover1:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


log%282%2C%28sqrt%28x%5E3-2x%5E2%2Bx%29%29%29=1%2Blog%282%2C%28x-1%29%29

There are, as nearly always, many different paths to solving this equation. My solution below is only one option.

(1) I would first express the constant "1" in terms of log base 2.

log%282%2C%28sqrt%28x%5E3-2x%5E2%2Bx%29%29%29=log%282%2C%282%29%29%2Blog%282%2C%28x-1%29%29

(2) On the right, use the rule that the sum of logs is the log of the product.

log%282%2C%28sqrt%28x%5E3-2x%5E2%2Bx%29%29%29=log%282%2C%282%28x-1%29%29%29

(3) The logs of the two expressions are equal, so the expressions are equal.

sqrt%28x%5E3-2x%5E2%2Bx%29=2%28x-1%29

(4) Square both sides to get rid of the radical.

x%5E3-2x%5E2%2Bx=4%28x-1%29%5E2

Instead of expanding on the right, simplify on the left....

x%28x%5E2-2x%2B1%29=4%28x-1%29%5E2
x%28x-1%29%5E2=4%28x-1%29%5E2
x%28x-1%29%5E2-4%28x-1%29%5E2=0
%28x-4%29%28x-1%29%5E2=0
%28x-4%29%28x%2B1%29%28x-1%29=0

The potential solutions are x=4, x=-1, and x=1.

(5) We need to check for extraneous solutions, because (1) at one point in the solution process we squared both sides of the equation and (2) log(A) is defined only if A is positive.

The expression log%282%2C%28x-1%29%29 in the original equation makes the solutions x=-1 and x=1 invalid; we need to see if x=4 satisfies the original equation.



1%2Blog%282%2C%284-1%29%29=log%282%2C%282%284%29-2%29%29=log%282%2C%286%29%29

x=4 satisfies the original equation, so it is the only solution.

ANSWER: x=4

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Please help me solve this question:log2{√(x³-2x²+x)}=1+log2(x-1)

 ------ Multiplying by LCD, 2 
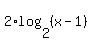 ------ Subtracting 2+%2A+log+%282%2C+%28x++-++1%29%29 from both sides

                    matrix%281%2C3%2C+%28x%28x++-++1%29%5E2%29%2F%28x++-++1%29%5E2%2C+%22=%22%2C+2%5E2%29 ------ Converting to EXPONENTIAL form 
At this point, with x - 1 in the denominator, the equation's "x" values can be ANY REAL NUMBER, EXCEPT 1.
                      matrix%281%2C3%2C+x%28x+-+1%29%5E2%2C+%22=%22%2C+4%28x+-+1%29%5E2%29 ------- Cross-multiplying
            
Therefore, x = 4 and also, x = 1 (DOUBLE-ROOT)
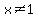However, since x CANNOT = 1 (x+%3C%3E+1, as stated above), the ONLY solution is: x = 4. 

Just to make sure that no errors were made, and since this involves LOGARITHMS and square roots, you'll need to CHECK to make sure that x = 4 is 
NOT an EXTRANEOUS solution.

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

log%282%2Csqrt%28x%5E3-2x%5E2%2Bx%29%29=1%2Blog%282%2C%28x-1%29%29

log%282%2Csqrt%28x%5E3-2x%5E2%2Bx%29%29+-+log%282%2C%28x-1%29%29=1

log%282%2Csqrt%28x%5E3-2x%5E2%2Bx%29%2F%28x-1%29%29=1........since log%282%2C2%29=1

log%282%2Csqrt%28x%5E3-2x%5E2%2Bx%29%2F%28x-1%29%29=log%282%2C2%29.........factor x%5E3-2x%5E2%2Bx=x+%28x+-+1%29%5E2

log%282%2Csqrt%28x+%28x+-+1%29%5E2%29%2F%28x-1%29%29=log%282%2C2%29

log%282%2C+%28%28x+-+1%29sqrt%28x%29%29%2F%28x-1%29%29=log%282%2C2%29........simplify

log%282%2C+sqrt%28x%29%29=log%282%2C2%29............since on both sides is log and base is same, we have
sqrt%28x%29=2.........square both sides

%28sqrt%28x%29%29%5E2=2%5E2
+x=4