Question 1194859: Assuming an alligator swallows stones with a mass 2.2 kg how much deeper, in millimeters, would it sink? Assume the alligator is initially floating and of 30% its body is above water and its body's surface area A= 1.2m^2; Use g=9.8 m/s^2, the p_water= 1,000 kg/m^3.
*I'm not sure which section this truly belongs too, but I desperately need help because I don't understand this question at all.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Assuming an alligator swallows stones with a mass 2.2 kg how much deeper, in millimeters,
would it sink? Assume the alligator is initially floating and of 30% its body
is above water and its body's surface area A= 1.2m^2; Use g=9.8 m/s^2, the p_water= 1,000 kg/m^3.
*I'm not sure which section this truly belongs too,
but I desperately need help because I don't understand this question at all.
~~~~~~~~~~~~~~~~
After reading this post, my impression is
that it is a "joke" entertainment problem.
By supporting its joking attitude, I will assume
that the alligator is a creation of a cubic form.
Then from given surface area, I can find "the length" of the alligator:
it is L = 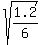 = 0.447 meters.
+----------------------------------------------------------------------------------------------+
| From it, I conclude that |
| 1) the total volume of the alligator is V = = 0.447 meters.
+----------------------------------------------------------------------------------------------+
| From it, I conclude that |
| 1) the total volume of the alligator is V =  = =  = 0.0894 m^3, |
| and |
| 2) its body is 0.7*0.447 = 0.313 m under the water surface. |
+----------------------------------------------------------------------------------------------+
0.7 of its volume is under water - - - hence, due to Archimedian law of floating,
the mass of the alligator is 0.7*0.0894*1000 = 62.58 kilograms.
After swallowing stones with the mass 2.2 kg, the mass of the alligator becomes 62.58 + 2.2 = 64.78 kilograms.
Supporting the joking nature of the problem, we assume, naturally, that the dimensions of the cubical alligator
do not change: it is still a cube with the edge length of 0.447 meters.
Now its body is = 0.0894 m^3, |
| and |
| 2) its body is 0.7*0.447 = 0.313 m under the water surface. |
+----------------------------------------------------------------------------------------------+
0.7 of its volume is under water - - - hence, due to Archimedian law of floating,
the mass of the alligator is 0.7*0.0894*1000 = 62.58 kilograms.
After swallowing stones with the mass 2.2 kg, the mass of the alligator becomes 62.58 + 2.2 = 64.78 kilograms.
Supporting the joking nature of the problem, we assume, naturally, that the dimensions of the cubical alligator
do not change: it is still a cube with the edge length of 0.447 meters.
Now its body is  = 0.324 meters under the water surface.
To find "how deep it would sink", take the difference 0.324 - 0.313 meters, and get the answer = 0.011 m = 11 millimeters. = 0.324 meters under the water surface.
To find "how deep it would sink", take the difference 0.324 - 0.313 meters, and get the answer = 0.011 m = 11 millimeters.
Solved.
Yes, as I said at the very beginning, you may consider it as a joke problem and my post as a joke solution.
The problem can be solved similarly by assuming that the alligator is a creature of spherical form (also as a joke).
Amusingly ?
- - - But, who knows, may be you will get a Nobel prize or something equivalent for this solution.
In such problems, the achievement is not measured in accuracy of your calculations, but in the power of your imagination . . .
|
|
|