Question 1194840: An urn contains 5 white and 7 black balls. Another urn contains 3 white and 9 black balls. If one ball from the first urn is selected at random and is transferred to the second urn, what is the probability that the ball drawn from the second urn gives a black?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52864)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An urn contains 5 white and 7 black balls. Another urn contains 3 white and 9 black balls.
If one ball from the first urn is selected at random and is transferred to the second urn,
what is the probability that the ball drawn from the second urn gives a black?
~~~~~~~~~~~~~~~~~~~~
First urn is (5W,7B) at the beginning, while second urn is (3W,9B).
After the transfer a ball from the first urn to the second urn,
- the 2nd urn becomes (4W,9B) with the probability of 5/(5+7) = 5/12,
if a white ball is transferred from the 1st urn,
or
- the 2nd urn becomes (3W,10B) with the probability of 7/(5+7) = 7/12,
if a black ball is transferred from the 1st urn.
Hence, the probability to draw a black ball from the second urn is
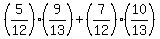 = = 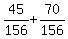 = = 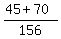 = = 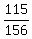 . ANSWER . ANSWER
Solved.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Define these events:- A = a white ball was selected from the first urn. It is transferred to the second urn.
- B = a black ball was selected from the first urn. It is transferred to the second urn.
- C = a black ball was selected from the second urn
Then we can form these probabilities:- P(A) = 5/12 since there are 5 white out of 5+7 = 12 total in the first urn
- P(B) = 7/12 since there are 7 black out of 5+7 = 12 total in the first urn
- P(C given A) = 9/13 because there are 9 black balls and 3white+9black+1extraWhite = 13 balls total in the second urn. Don't forget to add on that extra 1 white ball
- P(C given B) = 10/13 for similar reasoning as the previous probability. This time we have 1 extra black ball to get 9+1 = 10 total in the second urn.
The keyword "given" refers to conditional probability. It indicates that the prior event in question is known to already have happened.
Now use the law of total probability
P(C) = P(C and A) + P(C and B)
P(C) = P(C given A)*P(A) + P(C given B)*P(B)
P(C) = (9/13)*(5/12) + (10/13)*(7/12)
P(C) = (9*5)/(13*12) + (10*7)/(13*12)
P(C) = 45/156 + 70/156
P(C) = (45+70)/156
P(C) = 115/156
I would leave it in fraction form since it's the most exact.
If your teacher requires decimal form, then,
115/156 = 0.737179 approximately
Round this however your teacher instructs
This converts to 73.7179% approximately
Answer in fraction form is 115/156 (exact)
Answer in decimal form is 0.737179 (approximate)
Answer in percent form is 73.7179% (approximate)
Further reading about the law of total probability
https://www.probabilitycourse.com/chapter1/1_4_2_total_probability.php
Further reading about conditional probability
https://www.mathsisfun.com/data/probability-events-conditional.html
|
|
|