Question 1194827: The half-life of a radioactive substance is 1500 years.
a) What does the model look like if we use an exponential decay model (base e)? Explain what each part of the model represents.
b) If we start with 100 mg of the substance, how much of it will still be radioactive in 2000 years. Does your answer make sense?
c) If we start with 100 mg of the substance, how much of it will still be radioactive in 10,000 years. Does your answer make sense?
d) Will the 100mg ever completely dissipate (ie to 0 mg radioactive)? If so, when? Clearly explain why or why not.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The half-life of a radioactive substance is 1500 years.
a) What does the model look like if we use an exponential decay model (base e)?

Explain what each part of the model represents.
A = resulting amt after t time
Ao = initial amt of the substance (t=0)
k = decay rate of the substance (derived from the half-life)
t = time of decay
:
b) If we start with 100 mg of the substance, how much of it will still be radioactive in 2000 years.
find k, the decay rate, we know we have half of it left after 1500 yrs
k = 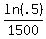
k = -.0004621
now we can solve for remaining substance after 2000 years
A = 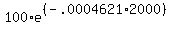
A = 39.68 mg
Does your answer make sense? yes we know it is less than half which is 50
:
c) If we start with 100 mg of the substance, how much of it will still be radioactive in 10,000 years.
A = 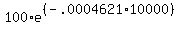
A = .9843 mg
Does your answer make sense?, yes, very little left after 10000 years
:
d) Will the 100mg ever completely dissipate (ie to 0 mg radioactive)? If so, when? Clearly explain why or why not.
Effectively, it will become so tiny, it can be considered 0, but theoretically it never reaches 0 as the time goes on to infinity. For example after 100000 yrs is will be about 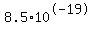 a tiny amt indeed! a tiny amt indeed!
|
|
|