Question 1194556: At a raffle, 2000 tickets are sold at $3 each for four prizes of $600, $250, $200, and $80. You buy one tickets.
A) What is the expected value of your gain?
B) interpret the results.
C) is this a fair game? Explain.
Answer by ikleyn(52848)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At a raffle, 2000 tickets are sold at $3 each for four prizes of $600, $250, $200, and $80. You buy one tickets.
A) What is the expected value of your gain?
B) interpret the results.
C) is this a fair game? Explain.
~~~~~~~~~~~~~~~
Bying one ticket, you have
- the probability of 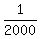 to win $600, or
- the probability of to win $600, or
- the probability of 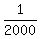 to win $250, or
- the probability of to win $250, or
- the probability of 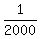 to win $200, or
- the probability of to win $200, or
- the probability of 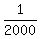 to win $80.
The expected value is then E = to win $80.
The expected value is then E = 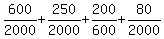 = = 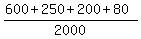 = = 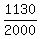 = 0.565 dollars.
Paying #3 for each ticket, the expected value of the game is $0.565 - $3 = -$2.435.
In other words, playing many times, the gamer loses $2.435 in any game, in average.
The game is unfair. = 0.565 dollars.
Paying #3 for each ticket, the expected value of the game is $0.565 - $3 = -$2.435.
In other words, playing many times, the gamer loses $2.435 in any game, in average.
The game is unfair.
Solved and explained.
|
|
|