Question 119455: I need to simplify each complex fraction. Please help this is confusing.
(w+3)/4w divided by(w-3)/2w
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 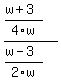
Remember the rule for dividing one fraction by another: Invert the denominator fraction and multiply:
 for all real p, q, r, and s, so for all real p, q, r, and s, so

Now you just multiply the numerators and the denominators the same way you would multiply any other two fractions:

Since there is a factor of 2w in both the numerator and denominator, we can eliminate that, so:

Since there are no more common factors in the numerator and denominator, we are done except for distributing the 2 in the denominator across the (w - 3) to remove the parentheses, thus:

Let's check our work:
We know that if  then then  , so if , so if  , then , then  must be true. must be true.

Now factor a 2 out of the binomial in the denominator resulting in:
 once you eliminate the common factor of (w - 3), and that verifies the answer. once you eliminate the common factor of (w - 3), and that verifies the answer.
Hope that helps.
John
|
|
|