Question 1194515: 1a). A small block of mass 2kg is suspended by two strings of lengths 0.6m and 0.8m
from two points 1m apart on a horizontal beam. Find the tension in each string.
1b). A vehicle of mass 6 x 10³ kg moving with a velocity of 43kmh-¹ collides with a
stationary vehicle of mass 185 x 10³ kg and they stick together and move in the same
direction. They then came to rest after moving through a distance of 3m. Calculate the
magnitude of retardation.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1a). A small block of mass 2kg is suspended by two strings of lengths 0.6m and 0.8m
from two points 1m apart on a horizontal beam. Find the tension in each string.
1b). A vehicle of mass 6 x 10³ kg moving with a velocity of 43kmh-¹ collides with a
stationary vehicle of mass 185 x 10³ kg and they stick together and move in the same
direction. They then came to rest after moving through a distance of 3m. Calculate the
magnitude of retardation.
~~~~~~~~~~~~~~
Problem 1a.
Let A and B be the points on the horizontal beam where the two strings are attached.
Let C be the point where the mass is attached to the strings.
Notice that the triangle ABC is the right-angled triangle: its sides |AC| = 0.6 m
and |BC| = 0.8 m are the legs and its side |AB| = 1 m is the hypotenuse, since
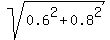 = = 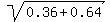 = = 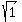 = 1 meter.
Let vector P along CA be the tension of CA and let vector Q along CB be the tention of CB.
Let p and q be the magnitudes of these vectors, respectively.
Since the mass is in equilibrium, the sum of x-components of vectors P and Q is zero:
Px + Qx = 0, or p*cos(A) = q*cos(B). (1)
Due to the same reason (Since the mass is in equilibrium), the sum of y-components of vectors P and Q
is numerically equal to the weight of the mass m*g = 2*10 = 20 newtons (here for simplicity
I take g = 10 m/s^2 for the gravity constant).
It gives the second equation
py + qy = 20 newtons, or p*sin(A) + q*cos(A) = 20. (2)
Now notice that from triangle ABC, sin(A) = 0.8/1 = 0.8; sin(B) = 0.6/1 = 0.6; cos(A) = 0.6/1 = 0.6; cos(B) = 0.8/1 = 0.8.
Hence, you can write equations (1) and (2) in this equivalent form
0.6p = 0.8q (3)
0.8p + 0.6q = 20 (4)
From equation (3), express p = = 1 meter.
Let vector P along CA be the tension of CA and let vector Q along CB be the tention of CB.
Let p and q be the magnitudes of these vectors, respectively.
Since the mass is in equilibrium, the sum of x-components of vectors P and Q is zero:
Px + Qx = 0, or p*cos(A) = q*cos(B). (1)
Due to the same reason (Since the mass is in equilibrium), the sum of y-components of vectors P and Q
is numerically equal to the weight of the mass m*g = 2*10 = 20 newtons (here for simplicity
I take g = 10 m/s^2 for the gravity constant).
It gives the second equation
py + qy = 20 newtons, or p*sin(A) + q*cos(A) = 20. (2)
Now notice that from triangle ABC, sin(A) = 0.8/1 = 0.8; sin(B) = 0.6/1 = 0.6; cos(A) = 0.6/1 = 0.6; cos(B) = 0.8/1 = 0.8.
Hence, you can write equations (1) and (2) in this equivalent form
0.6p = 0.8q (3)
0.8p + 0.6q = 20 (4)
From equation (3), express p = 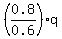 = = 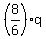 and substitute it into equation (4) and substitute it into equation (4)
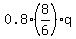 + + 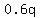 = 20 = 20
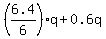 = 20 = 20
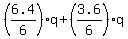 = 20 = 20
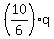 = 20
q = (6*20)/10 = 12 newtons.
p = = 20
q = (6*20)/10 = 12 newtons.
p = 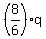 = = 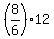 = 16 newtons.
ANSWER. The magnitudes of tensity are p= 16 N for CA and q= 12 N for CB. = 16 newtons.
ANSWER. The magnitudes of tensity are p= 16 N for CA and q= 12 N for CB.
Solved.
///////////////
Regarding your second problem, it is posed incorrectly, since it uses the term " retardation ",
which is not appropriate, not applicable and is IRRELEVANT in this context.
The appropriate terms are EITHER the " deceleration " OR the " friction force ".
NEVER SUBMIT more than one problem per post.
It is the RULE of this forum.
About the rules, read on web-page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you submit your problems.
|
|
|