Question 1194378: Suppose that an outbreak of cholera follows severe f;ooding in an isolated town of 2621 people, initially (Day0), 71 people are infected. Every day after, 12% of thoes still healthy fall ill.
By what day will 95% of the population be infected? (more specifically on the day before, fewer than this number are infected, but on this day, the number or more are infected)
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a = initial number of people infected = 71
r = 0.12 = growth rate in decimal form
b = 1 + r = 1+0.12 = 1.12 = growth factor
The template
y = a*b^x
becomes
y = 71*(1.12)^x
and this is an exponential model for the number who fall ill
x = number of days
y = number who are ill
The town has a population of 2621
95% of which is 0.95*2621 = 2489.95 which I'll round to the nearest whole number to get 2490
Once the town has 2490 ill people, it will reach an infection rate of about 95%.
Replace y with 2490 and solve for x.
You'll need logarithms to isolate the exponent.
y = 71*(1.12)^x
2490 = 71*(1.12)^x
2490/71 = (1.12)^x
(1.12)^x = 2490/71
(1.12)^x = 35.070423
Log[ (1.12)^x ] = Log[ 35.070423 ]
x*Log[ 1.12 ] = Log[ 35.070423 ]
x = Log[ 35.070423 ]/Log[ 1.12 ]
x = 31.389741
Let's check to see what happens when we plug in x = 31
y = 71*(1.12)^x
y = 71*(1.12)^31
y = 2382.413007
y = 2382
We don't reach the goal of 2490, but we get pretty close.
Now try x = 32
y = 71*(1.12)^x
y = 71*(1.12)^32
y = 2668.302568
y = 2668
We're now over the hurdle of 2490
Answer: Day 32
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that an outbreak of cholera follows severe flooding in an isolated town of 2621 people,
initially (Day0), 71 people are infected. Every day after, 12% of those still healthy fall ill.
By what day will 95% of the population be infected? (more specifically on the day before,
fewer than this number are infected, but on this day, the number or more are infected)
~~~~~~~~~~~~~~
The solution by the other tutor is incorrect.
This problem requires attentive reading before solving.
The governing formulas and the solution, as well as the answer are different
from that of the other tutor.
Let H(n) be the number of healphy people at the day n (those who are still healphy);
let I(n) be the number of ill people of the day n
(the cumulative sum of ill, formerly ill and death persons to the day n).
For the Day-0 we have, from the condition
H(0) = 2621 - 71 = 2550;
I(0) = 71
And in following days we have
H(n) = (1-0.12)*H(n-1) = 0.88H(n-1),
I(n) = 2621 - H(n),
in accordance with the problem's description.
Notice that these formulas and this setup are not the same as in the post by the other tutor:
+------------------------------------------------------------------+
| everyday decreasing the number of healthy people by 12%, |
| as described in the problem, is NOT THE SAME as |
| everyday increasing the number of ill people by 12%. |
+------------------------------------------------------------------+
Next, to solve the problem using formulas, notice that 95% of the population be infected means
that 5% of 2621 is still healthy, or 0.05*2621 = 131 is healthy (rounded).
So, we are looking to find n such that H(n) = 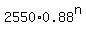 is still greater than 131: is still greater than 131:
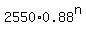 >= 131.
To solve this inequality, divide both sides by 2550 >= 131.
To solve this inequality, divide both sides by 2550
 >= >= 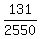 = 0.05137;
take the logarithm base 10 of both sides
n*log(0.88) >= log(0.05137)
express and calculate "n"
n >= = 0.05137;
take the logarithm base 10 of both sides
n*log(0.88) >= log(0.05137)
express and calculate "n"
n >= 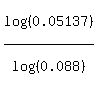 = 23.22321...
For the final answer, you should round this decimal number to the closest lesser integer, which is 23. = 23.22321...
For the final answer, you should round this decimal number to the closest lesser integer, which is 23.
Honestly, from your description, I am not sure, which of the two possible numbers, 23 or 24,
do you really want, but you can make your selection on your own.
In any case, the correct solution is in front of you.
Solved.
|
|
|