|
Question 1194325: The circumference and radius of a circle "T" are unknown. Two point A and B lie on circle whose arc length is 200 feet but the length of AB chord is 150 feet.
(A) Find the area of this segment from AB chord to AB curve?
(B) Can we find area of the circle "T" if we know the area of segment from AB chord to AB curve?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The circumference and radius of a circle "T" are unknown.
Two point A and B lie on circle whose arc length is 200 feet
but the length of AB chord is 150 feet.
(A) Find the area of this segment from AB chord to AB curve?
(B) Can we find area of the circle "T" if we know the area of segment from AB chord to AB curve?
~~~~~~~~~~~~~~~
In a coordinate plane make a sketch: draw a circle T (with unknown radius r);
mark the appropriate points A and B (A in Q1, B in the Q4 symmetrically to A about the x-axis).
Draw the chord AB.
Let the central angle for the arc AB be  radians.
So from the given part, you have these two equations radians.
So from the given part, you have these two equations
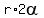 = 200 feet, or = 200 feet, or  = 100 (1) (from the arc length)
and = 100 (1) (from the arc length)
and
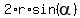 = 150, or = 150, or 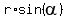 = 75. (2) (from the chord length).
Dividing equation (2) by equation (1), you get = 75. (2) (from the chord length).
Dividing equation (2) by equation (1), you get
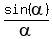 = = 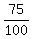 , or , or  = = 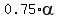 . (3)
This equation is not algebraic equation; it is transcendent equation and can not be solved
by the Algebra methods. But it can be solved numerically with any prescribed precision.
There are many solvers for solving such equations in the Internet.
I used one such free of charge common use solver at this link
https://www.wolframalpha.com/widgets/view.jsp?id=a7d8ae4569120b5bec12e7b6e9648b86
It gave me the value of . (3)
This equation is not algebraic equation; it is transcendent equation and can not be solved
by the Algebra methods. But it can be solved numerically with any prescribed precision.
There are many solvers for solving such equations in the Internet.
I used one such free of charge common use solver at this link
https://www.wolframalpha.com/widgets/view.jsp?id=a7d8ae4569120b5bec12e7b6e9648b86
It gave me the value of  = 1.2757 radians.
To check it, compare both sides of equation (3)
sin(1.2757) = 0.9568; 0.75*1.2757 = 0.9568,
so these values are consistent.
Next, knowing = 1.2757 radians.
To check it, compare both sides of equation (3)
sin(1.2757) = 0.9568; 0.75*1.2757 = 0.9568,
so these values are consistent.
Next, knowing  , we can find "r" from equation (1)
r = , we can find "r" from equation (1)
r = 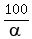 = = 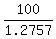 = 78.3883 (rounded).
+--------------------------------------------------------------+
| Now we have everything to answer the problem's questions. |
+--------------------------------------------------------------+
Question (A)
The area of the segment is the area of the sector minus the area of the triangle
area of the segment = = 78.3883 (rounded).
+--------------------------------------------------------------+
| Now we have everything to answer the problem's questions. |
+--------------------------------------------------------------+
Question (A)
The area of the segment is the area of the sector minus the area of the triangle
area of the segment = 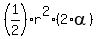 - -  =
= =
= 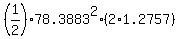 - - 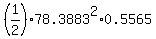 =
= 7838.8264 - 1709.7699 = 6129.0565 square units (rounded) ANSWER
Question (B)
After solving the problem, I just know the radius of the circle; therefore, I can calculate
the area of the circle. It is
area of the circle = =
= 7838.8264 - 1709.7699 = 6129.0565 square units (rounded) ANSWER
Question (B)
After solving the problem, I just know the radius of the circle; therefore, I can calculate
the area of the circle. It is
area of the circle =  = = 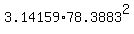 = 19304.2084 (rounded). ANSWER = 19304.2084 (rounded). ANSWER
The problem is solved in full.
|
|
|
| |