Question 1194310: How much sand must be added to 420lbs of concretemix that is 20% sand to have a mix that is 25% sand
Found 3 solutions by MathLover1, greenestamps, ikleyn:
Answer by MathLover1(20850)   (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is an informal alternative method for solving any 2-part "mixture" problem like this that is faster and easier than the standard algebraic solution shown by the other tutor -- if your mental arithmetic is good.
You are mixing 20% sand and 100% sand to get a mixture that is 25% sand.
Picture that as starting at 20% sand and moving towards 100% sand, stopping when you get to 25% sand.
The "distance" from 20 to 100 is 80; the "distance" from 20 to 25 is 5; 5/80 = 1/16.
In going from 20 towards 100 and stopping at 25, you have gone 1/16 of the total "distance". That means the 100% sand you are adding is 1/16 of the mixture.
That means the 420lb of mix that you started with is 15/16 of the mixture.
Since 1/16 is 1/15 of 15/16, the amount of sand you need to add is 1/15 of 420lb, which is 28lb.
ANSWER: 28 more pounds of sand
The words of explanation make this method sound long and tedious, but it is not. Without all the words, here are the calculations required to solve the problem:
100-20 = 80; 25-20 = 5; 5/80 = 1/16
1-1/16 = 15/16
(1/16)/(15/16) = 1/15
420(1/15) = 28
Answer by ikleyn(52790)  (Show Source):
You can put this solution on YOUR website! .
420 lbs of the 20% sand mixture contains 0.20*420 = 84 lbs of sand.
Hence, 420-84 = 336 lbs is another material (not sand): break stone and cement.
We want 336 lbs be 75% of the new mixture; hence, the total new mixture is 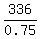 = 448 lbs.
It means that 448-420 = 28 lbs of sand should be added. ANSWER
Solved mentally, without using equations (only calculator :)
|
|
|
