.
40° is  of the full rotation.
So, the given area of
of the full rotation.
So, the given area of  cm^2 is
cm^2 is  of the total area of the circle.
It means that the total area of the circle is
of the total area of the circle.
It means that the total area of the circle is 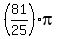 .
In other words,
.
In other words,  =
= 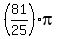 .
It implies. after reducing common factor
.
It implies. after reducing common factor  in both sides, that
in both sides, that
 =
= 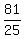 , or r =
, or r = 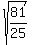 =
=  cm.
ANSWER. The radius is
cm.
ANSWER. The radius is  cm = 1.8 cm.
cm = 1.8 cm.
Solved.