You can
put this solution on YOUR website! .
In a binary communication system a zero and a one is transmitted with probability 0.6 and 0.4 respectively.
Due to error in the communication system a zero becomes a one with a probability 0.1 and a one becomes
a zero with a probability 0.08. Determine the probability
(i) of receiving a one and
(ii) that a one was transmitted when the received message is one
~~~~~~~~~~~~~~~
(i) P(receiving a one) = P(posting a zero)*P(zero becomes a one) + P(posting a one)*P(one remains one) =
0.6*0.1 + 0.4*(1-0.08) = 0.428. ANSWER
(ii) In this part, the problem asks about the conditional probability of transmitting one given that received
message is one. So, the denominator of the conditional fraction is P(receiving a one) = 0.428, just founded
in part (i).
The numerator of this fraction for conditional probability is
P(posting a one)*P(one remains one) = 0.4*(1-0.08) = 0.368.
Thus the final ANSWER for this part is P =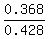 
= 0.8598 (rounded).
Solved.
