Question 1194161: In triangle ABC, tanA= 3/4, tanB= 1, and a=10; find b in simplest radical form.
At the end, I got b= (10sin(45))/sin(36.9). How would I put this final answer 11.8 into radical form?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In triangle ABC, tanA= 3/4, tanB= 1, and a=10; find b in simplest radical form.
At the end, I got b= (10sin(45))/sin(36.9). How would I put this final answer 11.8 into radical form?
~~~~~~~~~~~~~~~~~
Having tan(A) = y/x = 3/4, you may think that y= 3, x= 4 and therefore
sin(A) = 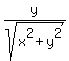 = = 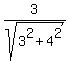 = 3/5.
Next, having tan(B) = 1, you conclude that B = 45 degrees; hence, sin(B) = = 3/5.
Next, having tan(B) = 1, you conclude that B = 45 degrees; hence, sin(B) =  .
After that, apply the sine law in the form .
After that, apply the sine law in the form
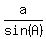 = = 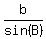 .
Everything except "b" is just known to you, so you write
b = .
Everything except "b" is just known to you, so you write
b = 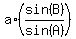 = and substitute what you just know = = and substitute what you just know = 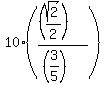 = = 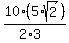 = = 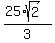 = 11.785 (approximately).
ANSWER. b = = 11.785 (approximately).
ANSWER. b = 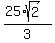 = 11.785 (approximately). = 11.785 (approximately).
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The fact that the problem asks for the answer in simplest radical form tells you you can't use a calculator to get an APPROXIMATE degree measure for angle A and try to work from there.
Your answer is numerically approximately correct; and you obviously got that result using the law of sines, so I think you know what you are doing. So I won't solve the problem for you, but rather point you in the right direction.
To get the exact answer in simplest radical form, note that tan(A)=3/4 means sin(A)=3/5 and cos(A)=4/5.
Now use the law of sines....
|
|
|