Question 1194138: Emmerson invests N$100,000.00 on a monthly basis, at the end of each month at an interest rate of 8.5% compounded quarterly.
a) How much will he have after 3.5 years
b) How much interest does he earn on a monthly basis? (Hint: Calculate the monthly average)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! payments at the end of each month = 100,000.
interest rate is 8.5% compounded quarterly.
the quarterly interest rate is 8.5% / 4 = 2.125%.
the number of quarters is equal to 3.5 years * 4 = 14.
the future value of the stream of these payments is equal to 1,610,814.56.
the total interest earned is 1,610,814.56 minus 14 * 100,000 = 210,814.56.
divide that by 14 months to get average interest earned per month = 15,058.18.
the ti-ba-ii business analyst calculator was used to get these results.
comparable results can be obtained online by using the arachnoid financial calculator found at https://arachnoid.com/finance/index.html
the results from using this calculator are shown below

Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Emmerson invests N$100,000.00 on a monthly basis, at the end of each month at an interest rate of 8.5% compounded quarterly.
a) How much will he have after 3.5 years
b) How much interest does he earn on a monthly basis? (Hint: Calculate the monthly average)
~~~~~~~~~~~~~~~~~~~~~~
The solution by @Theo is incorrect, since in calculations he mistakenly considers N$100,000.00 as quarterly deposits,
while they are the monthly contributions.
In my post below, I am placing a correct solution for question (a), ONLY.
Question (b) is posed in unclear way, so I will not answer it, at all.
As I understand, this account works as follows:
Emmerson invests 100,000 every month; but the bank makes compounding only once in 3 months.
So, every month investments of 100,000 wait to the end of the quarter, and only after that
the compounding is made and 300000 is added.
So, it works as an usual Ordinary Annuity quarterly compound account with 300,000 quarterly deposits.
The standard general formula for Ordinary Annuity is
FV =  , (1)
where FV is the future value of the account; P is the quarterly payment (deposit);
1+r is the quarterly growth factor;
n is the number of deposits (= the number of years multiplied by 3.5, in this case).
Under the given conditions, P = 300,000; r = 0.085/4; n = 4*3.5 = 14.
So, according to the formula (1), Emmerson will get at the end of the 14 months
FV = , (1)
where FV is the future value of the account; P is the quarterly payment (deposit);
1+r is the quarterly growth factor;
n is the number of deposits (= the number of years multiplied by 3.5, in this case).
Under the given conditions, P = 300,000; r = 0.085/4; n = 4*3.5 = 14.
So, according to the formula (1), Emmerson will get at the end of the 14 months
FV = 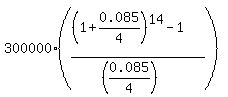 = $4832444 dollars.
Note that Emmerson deposits only 3*100000*4*3.5 = 4200000 dollars in 3.5 years.
The rest 4832444 - 4200000 = 632444 is the interest which the account earns/accumulates in 3.5 years. = $4832444 dollars.
Note that Emmerson deposits only 3*100000*4*3.5 = 4200000 dollars in 3.5 years.
The rest 4832444 - 4200000 = 632444 is the interest which the account earns/accumulates in 3.5 years.
-----------------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
----------------
It is just the second time this problem is posted to the forum.
First time it was posted and I answered it under this link
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1194023.html
|
|
|