Question 1194023: Emmerson invests N$100,000.00 on a monthly basis, at the end of each month at an interest rate of 8.5% compounded quarterly.
a) How much will he have after 3.5 years?
b) How much interest does he earn on a monthly basis? (Hint: Calculate the monthly average.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! a key requirement is to get the interest rate per month.
8.5% per year comounded quarterly = 8.5 divided by 4 = 2.125% per quarter.
the growth factor per quarter is that divided by 100 and added to 1 to get 1.02125 per quarter.
the growth factor per month is that raised to the 1/3 power to get 1.02125 ^ (1/3) = 1.007033744.
subtract 1 from that and multiply it by 100 to .7033744% per month.
use a financial calculator to find the future value of that for 3.5 years.
inputs are:
present value = 0
number of months = 3.5 years * 12 = 42.
interest rate per month = .7033744%
payment amount = -100,000 at the end of each month
solve for future value to get future value = 4,866,513.568.
the total payments are 42 * 100,000 = 4,200,000
the total interest is 4,866,513.568 minus 4,200,000 = 666,513.568.
the average monthly interest is 666,513.568 / 42 = 15,869.37067.
that's what i get.
let me know if you have any questions or concerns.
theo
Answer by ikleyn(52783)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I have different view on how this account works;
therefore, my solution for question (a) is different from that by @Theo.
In my post below, I am placing my solution for question (a), ONLY.
Question (b) is posed in unclear way, so I will not answer it, at all.
As I understand, this account works as follows:
Emmerson invests 100,000 every month; but the bank makes compounding only once in 3 months.
So, every month investments of 100,000 wait to the end of the quarter, and only after that
the compounding is made and 300000 is added.
So, it works as an usual Ordinary Annuity quarterly compound account with 300,000 quarterly deposits.
The standard general formula for Ordinary Annuity is
FV =  , (1)
where FV is the future value of the account; P is the quarterly payment (deposit);
1+r is the quarterly growth factor;
n is the number of deposits (= the number of years multiplied by 3.5, in this case).
Under the given conditions, P = 300,000; r = 0.085/4; n = 4*3.5 = 14.
So, according to the formula (1), Emmerson will get at the end of the 14 months
FV = , (1)
where FV is the future value of the account; P is the quarterly payment (deposit);
1+r is the quarterly growth factor;
n is the number of deposits (= the number of years multiplied by 3.5, in this case).
Under the given conditions, P = 300,000; r = 0.085/4; n = 4*3.5 = 14.
So, according to the formula (1), Emmerson will get at the end of the 14 months
FV = 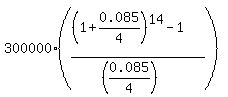 = $4832444 dollars.
Note that Emmerson deposits only 3*100000*4*3.5 = 4200000 dollars in 3.5 years.
The rest 4832444 - 4200000 = 632444 is the interest which the account earns/accumulates in 3.5 years. = $4832444 dollars.
Note that Emmerson deposits only 3*100000*4*3.5 = 4200000 dollars in 3.5 years.
The rest 4832444 - 4200000 = 632444 is the interest which the account earns/accumulates in 3.5 years.
-----------------
So, the major difference between my solution and that by @Theo is that in my solution
monthly current deposits wait for the end of the quarter to be compounded, while @Theo
compounds them on the monthly basis, although it is not quite equivalent, and the bank does not work this way.
The difference of $4866514 - $4832444 = $34,070 is the consequence of this inequivalence.
=================
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
|
|
|