 has positive concavity when its graph, a parabola, opens upward,
which is when the coefficient of x2 is positive, which means
greater than 0, so solve the inequality for k:
has positive concavity when its graph, a parabola, opens upward,
which is when the coefficient of x2 is positive, which means
greater than 0, so solve the inequality for k:
 Also to pass through the x-axis twice, its discriminant must
be positive to give it two unique real zeros. So simplify
and solve this inequality for k:
Also to pass through the x-axis twice, its discriminant must
be positive to give it two unique real zeros. So simplify
and solve this inequality for k:

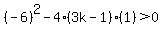 Now look at the two solutions to those two inequalities and
fill in fractions in the two blanks.
___ < k < ___
Edwin
Now look at the two solutions to those two inequalities and
fill in fractions in the two blanks.
___ < k < ___
Edwin