Question 1193769: How many quarterly payments of P15,000 will be necessary to pay off a debt of 175,000 if the interest rate charged is 8% converted quarterly?
Found 2 solutions by proyaop, ikleyn:
Answer by proyaop(69)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Determine the Quarterly Interest Rate:**
* Annual Interest Rate: 8%
* Quarterly Interest Rate: 8% / 4 = 2% or 0.02
**2. Calculate the Number of Payments**
* This requires an iterative approach. We can use a spreadsheet or a financial calculator for this.
**Here's a simplified explanation of the process:**
* **Start with an initial guess:** Let's assume 12 quarterly payments.
* **Calculate the present value of an annuity:**
* Use the formula: PV = PMT * [(1 - (1 + r)^-n) / r]
* PV = Present Value (what the loan is worth today)
* PMT = Quarterly Payment (P15,000)
* r = Quarterly interest rate (0.02)
* n = Number of payments (12 in this case)
* **Compare the calculated present value to the actual debt:**
* If the calculated present value is less than the actual debt, the number of payments is insufficient.
* If the calculated present value is greater than the actual debt, the number of payments is excessive.
* **Adjust the number of payments accordingly and repeat the calculation.**
**Using a financial calculator or spreadsheet software (like Excel or Google Sheets) with the PV function, you'll find that it takes approximately 14 quarterly payments to pay off the debt of P175,000 with quarterly payments of P15,000 at an 8% annual interest rate.**
**Note:** This calculation assumes that the interest is compounded quarterly and that the payments are made at the end of each quarter.
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many quarterly payments of P15,000 will be necessary to pay off a debt
of 175,000 if the interest rate charged is 8%  compounded quarterly? compounded quarterly?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Use the standard formula for the quarterly payment for a loan
P =  ,
where L is the loan amount; r = ,
where L is the loan amount; r =  = 0.02 is the effective quarterly compounding interest rate;
n is the number of payments; P is the quarterly payment.
In this problem P = $15000; r = = 0.02 is the effective quarterly compounding interest rate;
n is the number of payments; P is the quarterly payment.
In this problem P = $15000; r =  = 0.02.
Substitute these values into the formula and get for quarterly payment
15000 = = 0.02.
Substitute these values into the formula and get for quarterly payment
15000 =  .
In this equation, n is the unknown: we should find n from this equation.
Simplify step by step .
In this equation, n is the unknown: we should find n from this equation.
Simplify step by step
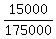 = = 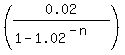 ,
0.085714286 = ,
0.085714286 = 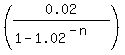 , ,
 = = 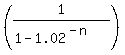 ,
4.2857143 = ,
4.2857143 = 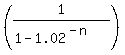 , ,
 = =  ,
0.233333333 = ,
0.233333333 =  , ,
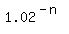 = 1 - 0.233333333, = 1 - 0.233333333,
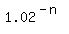 = 0.766666667, = 0.766666667,
 = 0.766666667,
1.02^n = 1/0.766666667,
1.02^n = 1.304347826
,
n*log(1.02) = log(1.304347826),
n = = 0.766666667,
1.02^n = 1/0.766666667,
1.02^n = 1.304347826
,
n*log(1.02) = log(1.304347826),
n = 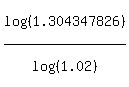 = 13.4.
So, 13 full semi-annual payments should be made of 2,000 each,
and then the last,14-th payment, should be made of the lesser amount.
ANSWER. 13 full semi-annual payments should be made of 2,000 each,
and then the last, 14-th payment, should be made of the lesser amount.
The total number of semi-annual payments is 14. = 13.4.
So, 13 full semi-annual payments should be made of 2,000 each,
and then the last,14-th payment, should be made of the lesser amount.
ANSWER. 13 full semi-annual payments should be made of 2,000 each,
and then the last, 14-th payment, should be made of the lesser amount.
The total number of semi-annual payments is 14.
Solved.
|
|
|