Question 1193768: A P38,000 loan bears interest at 10% compounded semi-annually and is to be repaid in semi-annual payments of P2,000 each.
a. How many semi-annual payments must be the debtor make?
b. What smaller final payment should he make six months after the last payment of P2,000 is made?
Found 2 solutions by proyaop, ikleyn:
Answer by proyaop(69)   (Show Source):
You can put this solution on YOUR website! **a. Determine the Number of Semi-Annual Payments**
* **Find the effective semi-annual interest rate:**
* Semi-annual interest rate = (1 + Annual Interest Rate / Number of compounding periods per year)^(Number of compounding periods per year) - 1
* Semi-annual interest rate = (1 + 0.10 / 2)^(2) - 1
* Semi-annual interest rate = 0.0525 or 5.25%
* **Use a financial calculator or spreadsheet software (like Excel or Google Sheets) to determine the number of payments.**
* **In Excel, you can use the NPER function:**
* `=NPER(rate, pmt, pv, [fv], [type])`
* rate: Semi-annual interest rate (0.0525)
* pmt: Payment amount (-2000)
* pv: Present value (38000)
* fv: Future value (0, as the loan will be fully paid off)
* type: 0 for payments at the end of each period (default)
* This will give you the number of semi-annual payments required to repay the loan.
**b. Calculate the Smaller Final Payment**
1. **Calculate the remaining balance after the last full payment of P2,000:**
* This involves calculating the remaining balance after the number of full payments determined in part (a). You can use the financial calculator or spreadsheet functions like `FV` (future value) to calculate the remaining balance after these payments.
2. **Calculate the interest accrued on the remaining balance:**
* Multiply the remaining balance by the semi-annual interest rate.
3. **Calculate the final payment:**
* Final payment = Remaining balance + Interest accrued on the remaining balance
**Note:**
* This approach provides a general framework for solving this type of loan repayment problem.
* The specific calculations will require the use of financial tools or software.
Let me know if you'd like to explore the calculations using a specific financial calculator or spreadsheet software.
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
A P38,000 loan bears interest at 10% compounded semi-annually and is to be repaid
in semi-annual payments of P2,000 each.
a. How many semi-annual payments must be the debtor make?
b. What smaller final payment should he make six months after the last payment
of P2,000 is made?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Use the standard formula for the semi-annual payment for a loan
P =  ,
where L is the loan amount; r =  is the effective semi-annual compounding interest rate;
n is the number of payments; P is the semi-annual payment.
In this problem P = $2000; r = = 0.05.
Substitute these values into the formula and get for semi-annual payment
2000 =  .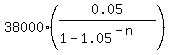
In this equation, n is the unknown: we should find n from this equation.
Simplify step by step
 =  ,
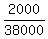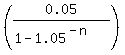0.052631579 = ,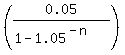
 =  ,
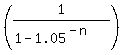1.05263158 = ,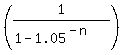
 =  ,
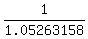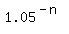0.95 = ,
 = 1 - 0.9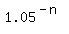5,
= 0.05,
 = 0.05,
1.05^n = 1/0.05,
1.05^n = 20,
n*log(1.05) = log(20),
n =  = 61.4.
So, 61 full semi-annual payments should be made of 2,000 each,
and then the last,62-th payment, should be made of the lesser amount.
ANSWER. 61 full semi-annual payments should be made of 2,000 each,
and then the last, 62-th payment, should be made of the lesser amount.
The total number of semi-annual payments is 62.
Solved.
|
|
|
