Question 1193612: If a loan of ₱60,000 is to be settled by 3,200 monthly payments for 2
years, what interest rate compounded monthly is charged on the loan?
Found 2 solutions by yurtman, ikleyn:
Answer by yurtman(42)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the interest rate compounded monthly, we use the formula for the monthly payment of a loan under compound interest:
\[
M = \frac{P \cdot r \cdot (1 + r)^n}{(1 + r)^n - 1}
\]
Where:
- \( M \) = monthly payment (\( 3,200 \))
- \( P \) = principal (\( 60,000 \))
- \( r \) = monthly interest rate (to be determined)
- \( n \) = total number of payments (\( 2 \, \text{years} \times 12 = 24 \))
---
### Step 1: Plug in Known Values
Substituting \( M = 3,200 \), \( P = 60,000 \), and \( n = 24 \):
\[
3,200 = \frac{60,000 \cdot r \cdot (1 + r)^{24}}{(1 + r)^{24} - 1}
\]
Simplify:
\[
3,200 \cdot \left( (1 + r)^{24} - 1 \right) = 60,000 \cdot r \cdot (1 + r)^{24}
\]
---
### Step 2: Rearrange for \( r \)
Rewriting the equation:
\[
\frac{3,200}{60,000} = \frac{r \cdot (1 + r)^{24}}{(1 + r)^{24} - 1}
\]
\[
\frac{3,200}{60,000} = 0.05333
\]
So:
\[
0.05333 = \frac{r \cdot (1 + r)^{24}}{(1 + r)^{24} - 1}
\]
---
### Step 3: Solve for \( r \) Numerically
This equation cannot be solved algebraically, so we solve it numerically or with an iterative approach:
#### Iterative Approximation:
1. Start with an initial guess for \( r \).
2. Compute the left and right sides of the equation.
3. Adjust \( r \) until both sides are approximately equal.
After solving numerically, the monthly interest rate \( r \) is approximately:
\[
r = 0.01 \, \text{(or 1% per month)}.
\]
---
### Step 4: Convert to Annual Interest Rate
The nominal annual interest rate is:
\[
\text{Annual Rate} = r \cdot 12 = 0.01 \cdot 12 = 0.12 \, \text{(or 12% per year)}.
\]
---
### Final Answer:
The interest rate charged on the loan is **12% per year compounded monthly**.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a loan of ₱60,000 is to be settled by 3,200 monthly payments for 2
years, what interest rate compounded monthly is charged on the loan?
~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by the other tutor is WRONG.
So, I came to bring a correct solution.
Write a loan equation
M = 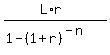 ,
where
M is the monthly payment;
L is the loaned amount;
r is the monthly effective rate as a decimal;
n is the number of payments (= the number of months).
In our case this equation takes the form
3200 = ,
where
M is the monthly payment;
L is the loaned amount;
r is the monthly effective rate as a decimal;
n is the number of payments (= the number of months).
In our case this equation takes the form
3200 = 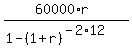 ,
or ,
or
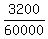 = = 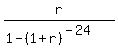 .
0.053333333 = .
0.053333333 = 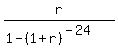 .
In this equation, r is the unknown.
Such equation is unsolvable algebraically, so use the numerical methods.
You may use any of numerous online calculators.
I used DESMOS at www.desmos.com/calculator
It gave me r = 0.02077, approximately.
Here is the link to the DESMOS solution.
https://www.desmos.com/calculator/aivq2p1eli
Click on the intersection point to get its coordinates.
This value r = 0.02077 is the monthly effective rate - - - so, the annual nominal rate is 12 times this value .
In this equation, r is the unknown.
Such equation is unsolvable algebraically, so use the numerical methods.
You may use any of numerous online calculators.
I used DESMOS at www.desmos.com/calculator
It gave me r = 0.02077, approximately.
Here is the link to the DESMOS solution.
https://www.desmos.com/calculator/aivq2p1eli
Click on the intersection point to get its coordinates.
This value r = 0.02077 is the monthly effective rate - - - so, the annual nominal rate is 12 times this value
 = 12*0.02077 = 0.24924, or about 0.25,
which corresponds to 25%.
ANSWER. In this problem, the annual interest rate is about 25% compounded monthly.
Surely, from the usual common sense, this rate is extremely high,
but it tells only that this problem is Math - - - not from real life. = 12*0.02077 = 0.24924, or about 0.25,
which corresponds to 25%.
ANSWER. In this problem, the annual interest rate is about 25% compounded monthly.
Surely, from the usual common sense, this rate is extremely high,
but it tells only that this problem is Math - - - not from real life.
Solved.
---------------------
To check my solution, I substituted this value r= 0.02077
into the loan function f(r) = 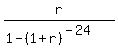 = = 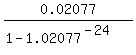 .
It returns the value 0.053333396, which is quite close to 0.053333333, so my solution is confirmed.
To check the solution from the other tutor, I substituted his value r= 0.01
into the loan function f(r) = .
It returns the value 0.053333396, which is quite close to 0.053333333, so my solution is confirmed.
To check the solution from the other tutor, I substituted his value r= 0.01
into the loan function f(r) = 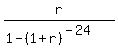 = = 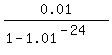 .
It returns the value 0.047073, which is not close to .
It returns the value 0.047073, which is not close to 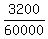 = 0.053333333.
So, the other's tutor solution is wrong, which is confirmed. = 0.053333333.
So, the other's tutor solution is wrong, which is confirmed.
|
|
|