Question 1193476: You have $400,000 saved for retirement. Your account earns 9% interest compounded monthly. How much will you be able to pull out each month, if you want to be able to take withdrawals for 15 years?
$
You can afford a $1400 per month mortgage payment. You've found a 30 year loan at 7% interest compounded monthly.
a) How big of a loan can you afford?
$
b) How much total money will you pay the loan company?
$
c) How much of that money is interest?
$
Found 2 solutions by ElectricPavlov, ikleyn:
Answer by ElectricPavlov(122)   (Show Source):
You can put this solution on YOUR website! **a) Existence of Maximum and Minimum Points**
* **Closed and Bounded Set:** The constraint 2x² + y² = 6 defines an ellipse, which is a closed and bounded set in the plane.
* **Continuous Function:** The function f(x, y) = x*y² is a polynomial, hence continuous everywhere, and therefore continuous on the ellipse.
**Extreme Value Theorem:** Since f is continuous on a closed and bounded set (the ellipse), the Extreme Value Theorem guarantees that f attains both a maximum and a minimum value on that set.
* **No Stationary Points:**
* ∇f(x, y) = (y², 2xy)
* ∇f(x, y) = 0 only at (0, 0)
* The point (0, 0) does not satisfy the constraint 2x² + y² = 6.
**b) Lagrange Multipliers**
* **Lagrangian:**
L(x, y, λ) = x*y² - λ(2x² + y² - 6)
* **Partial Derivatives:**
* ∂L/∂x = y² - 4λx
* ∂L/∂y = 2xy - 2λy
* ∂L/∂λ = -(2x² + y² - 6)
* **System of Equations:**
* y² - 4λx = 0
* 2xy - 2λy = 0
* 2x² + y² = 6
* **Solving the System:**
* From the second equation:
* 2y(x - λ) = 0
* y = 0 or x = λ
* If y = 0, then from the constraint:
* 2x² = 6
* x = ±√3
* This gives us the points (±√3, 0)
* If x = λ, then from the first equation:
* y² - 4x² = 0
* y² = 4x²
* Substitute into the constraint:
* 2x² + 4x² = 6
* x = ±1
* If x = 1, then y² = 4, so y = ±2
* If x = -1, then y² = 4, so y = ±2
* This gives us the points (1, 2), (1, -2), (-1, 2), and (-1, -2)
* **Evaluate f at the Critical Points:**
* f(√3, 0) = 0
* f(-√3, 0) = 0
* f(1, 2) = 4
* f(1, -2) = 4
* f(-1, 2) = -4
* f(-1, -2) = -4
* **Conclusion:**
* **Maximum Value:** 4 at (1, 2) and (1, -2)
* **Minimum Value:** -4 at (-1, 2) and (-1, -2)
**c) Definition Set: 2x² + y² ≤ 6**
* **Interior Points:** We already determined that there are no stationary points within the interior of the ellipse.
* **Boundary:** The analysis in part (b) already considered the boundary (2x² + y² = 6).
* **Conclusion:** The maximum and minimum values remain the same as in part (b) because the boundary points still provide the extrema.
**d) Function h(x, y) = 4 - x² - y²**
**i) Level Curve and Gradient at P(1, -1)**
* **Level Curve:**
* f(1, -1) = 1
* The level curve of f at P(1, -1) is the set of points (x, y) such that f(x, y) = 1, which is the curve x*y² = 1.
* **Gradient of h:**
* ∇h(x, y) = (-2x, -2y)
* ∇h(1, -1) = (-2, 2)
**ii) Directional Derivative**
* **Unit Vector in the Direction of v:**
* ||v|| = √((-3)² + 4²) = 5
*
Answer by ikleyn(52767)  (Show Source):
You can put this solution on YOUR website! .
You have $400,000 saved for retirement. Your account earns 9% interest compounded monthly.
How much will you be able to pull out each month, if you want to be able to take withdrawals for 15 years?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The content in the post by @ElectricPavlov is irrelevant to the posed problem,
so the best that you can do with it is to ignore it.
Here, in this my post, I will solve first problem for you.
There are two basic scenarios for money withdrawal from sinking fund:
(1) doing it at the beginning of the month, and
(2) doing it at the end of the month.
In Finance, there are two different formulas for these scenarios, and the problem,
if posed correctly, should declare it explicitly, which scenario is under the question.
For living, it is more traditional scenario to make withdrawals at the beginning of the month.
So, I will consider this case and will use relevant formula.
For withdrawals made at the beginning of each month, the general formula for an Annuity Due sinking fund is
A =  .
Here A is the initial amount at the account;
W is the monthly withdrawn value at the beginning of each month;
r is the effective monthly rate r = 0.09/12 presented as a decimal;
p = 1 + r and n is the number of withdrawing periods (months, in this case).
In this problem, A = $400,000 is given;
W is the unknown;
the monthly rate is r = 0.09/12 = 0.0075,
p = 1 + 0.0075 = 1.0075,
the number of withdrawals (= the number of months) is n = 15*12 = 180. So
400000 =  .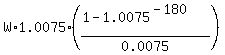
The factor 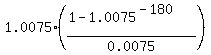 is equal to 99.3328594; therefore
W =  = 4026.86 dollars.
Thus you will be able to withdraw $4026.86485 every month (rounded to the closest lesser cent) during 15 years.
Solved.
-------------------------
In this problem, the starting principal of $400,000 looks as moderate, but the
monthly withdrawal of about $4000 looks as significant.
It is because the annual interest of 9% compounded monthly for 15 years in a row
is unrealistically high.
=========================
Post-notes after the solution
(1) The fact, that the problem does not declare, when withdrawals are made, tells me
that the problem composer does not know how to pose such problems correctly.
(2) In the future, NEVER post more than one problem per post.
It is the rule of this forum and the rule of EVERY forum for mathematical help.
Asking one question/(one problem) at a time is also the rule of normal, mutually polite communication.
Posting many questions at a time is a sign of mental disorder and general bad manners.
|
|
|
