|
Question 1193474: How much should you invest each month in order to have $700,000 if your rate of return is 2.1% compounded monthly and you want to achieve your goal in 40 years?
How much interest will you earn?
How much should you invest each month in order to have $700,000 if you want to achieve your goal in 20 years?
If you deposit the amount you need to achieve your goal in 20 years, how much will your savings be worth after 10 years?
Found 2 solutions by yurtman, ikleyn:
Answer by yurtman(42)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. 40-Year Goal**
* **Find Monthly Interest Rate:**
* Monthly Interest Rate = Annual Interest Rate / 12
* Monthly Interest Rate = 2.1% / 12 = 0.175% = 0.00175
* **Calculate Number of Months:**
* Number of Months = 40 years * 12 months/year = 480 months
* **Use the Future Value of an Ordinary Annuity Formula:**
* Future Value (FV) = P * (((1 + r)^n - 1) / r)
* Where:
* FV = Future Value ($700,000)
* P = Monthly Payment (unknown)
* r = Monthly Interest Rate (0.00175)
* n = Number of Periods (480 months)
* **Rearrange the formula to solve for P:**
* P = FV / (((1 + r)^n - 1) / r)
* P = $700,000 / (((1 + 0.00175)^480 - 1) / 0.00175)
* P ≈ $700,000 / 453.03
* P ≈ $1545.35
**Therefore, you should invest approximately $1545.35 each month for 40 years to reach $700,000.**
**2. Interest Earned**
* **Total Contributions:** $1545.35/month * 480 months = $738,168
* **Interest Earned:** $700,000 - $738,168 = -$38,168
**Note:** In this scenario, you would actually have contributed more than the final goal. This highlights the importance of investment growth and the power of compounding over long periods.
**3. 20-Year Goal**
* **Calculate Number of Months:**
* Number of Months = 20 years * 12 months/year = 240 months
* **Use the Future Value of an Ordinary Annuity Formula (same as above):**
* P = $700,000 / (((1 + 0.00175)^240 - 1) / 0.00175)
* P ≈ $700,000 / 132.19
* P ≈ $5295.63
**Therefore, you should invest approximately $5295.63 each month for 20 years to reach $700,000.**
**4. Savings after 10 Years (Investing $5295.63 Monthly)**
* **Calculate Number of Months:**
* Number of Months = 10 years * 12 months/year = 120 months
* **Use the Future Value of an Ordinary Annuity Formula:**
* Future Value (FV) = $5295.63 * (((1 + 0.00175)^120 - 1) / 0.00175)
* FV ≈ $5295.63 * 132.19
* FV ≈ $700,000
**Therefore, if you invest $5295.63 each month for 10 years at a 2.1% monthly compounded rate, your savings will be worth approximately $700,000.**
**Disclaimer:**
* These calculations are based on consistent monthly contributions and a fixed interest rate.
* Actual investment returns may vary and are not guaranteed.
* This information is for illustrative purposes only and does not constitute financial advice.
**Key Takeaways:**
* The longer your investment horizon, the lower your monthly contributions can be to achieve the same goal.
* Even with a relatively low interest rate, consistent monthly contributions can lead to significant savings growth over time, thanks to the power of compounding.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) How much should you invest each month in order to have $700,000 if your rate of return is 2.1% compounded monthly and you want to achieve your goal in 40 years?
How much interest will you earn?
(b) How much should you invest each month in order to have $700,000 if you want to achieve your goal in 20 years?
(c) If you deposit the amount you need to achieve your goal in 20 years, how much will your savings be worth after 10 years?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Calculations in the post by the tutor @yurtman are INCORRECT.
It is why his numbers are absurdist.
I came to bring a correct solution.
I will solve here parts (a) and (b). I do not like when many problems/questions are packed in one post.
By the way, it contradicts to the rules of this forum.
Part (a)
This problem is to determine the amount of monthly payments/deposits.
Since the problem does not specifies when the monthly payments are due, I will assume that
the monthly payments are at the end of each month. Then it is a classic Ordinary Annuity saving plan.
The general formula to start (which is a PREREQUISITE and which you should know from your textbook) is
FV =  ,
Here FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly effective rate presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
Here FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly effective rate presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $700,000; r = 0.021/12; n = 40*12 = 480.
So, according to the formula (1), you get for the monthly payment
P = . (1)
Under the given conditions, FV = $700,000; r = 0.021/12; n = 40*12 = 480.
So, according to the formula (1), you get for the monthly payment
P = 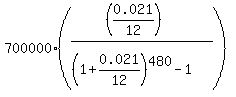 = $931.80 (rounded).
The interest is 700000 - 480*931.80 = 252,736 dollars.
Answer. The necessary monthly deposit is $931.80.
The interest is @252,736.
Part (b)
Use the same formula (1) for the monthly payment
This time, your input data is FV = $700,000; r = 0.021/12; n = 20*12 = 240.
So, according to the formula (1), you get for the monthly payment
P = = $931.80 (rounded).
The interest is 700000 - 480*931.80 = 252,736 dollars.
Answer. The necessary monthly deposit is $931.80.
The interest is @252,736.
Part (b)
Use the same formula (1) for the monthly payment
This time, your input data is FV = $700,000; r = 0.021/12; n = 20*12 = 240.
So, according to the formula (1), you get for the monthly payment
P = 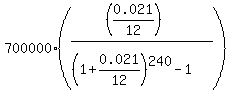 = $2349.43 (rounded).
Answer. The necessary monthly deposit is $2349.43. = $2349.43 (rounded).
Answer. The necessary monthly deposit is $2349.43.
Solved.
---------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
|
|
|
| |