Question 1193440: A shipment of 10 items has two defective and eight non defective units. In the inspection of the shipment , a sample of units will be selected and tested. If a defective unit is found , the shipment of 10 units will be rejected.If a sample of four is selected , what is the probability that the shipment will be rejected?
Found 3 solutions by CPhill, ikleyn, greenestamps:
Answer by CPhill(1987)   (Show Source):
You can put this solution on YOUR website! **1. Define the Probability of Rejection:**
* The probability of rejecting a shipment is the probability of finding at least one defective unit in the sample.
**2. Calculate the Probability of Not Rejecting:**
* The probability of not rejecting a shipment is the probability of finding no defective units in the sample.
**3. Determine the Sample Size:**
* We need to find the sample size (n) that satisfies the following condition:
Probability of rejecting the shipment ≥ 0.90
1 - Probability of not rejecting the shipment ≥ 0.90
Probability of not rejecting the shipment ≤ 0.10
**4. Calculate the Probability of Not Rejecting (for a given sample size n):**
* The probability of not rejecting a shipment is the probability of selecting only non-defective units in the sample.
* This can be calculated using the hypergeometric distribution:
Probability of not rejecting = (Number of ways to choose n non-defective units from 8 non-defective units) / (Total number of ways to choose n units from 10 total units)
Probability of not rejecting = (8Cn) / (10Cn)
**5. Find the Sample Size (n) by Trial and Error:**
* Start with a small sample size (e.g., n = 1) and calculate the probability of not rejecting.
* Increase the sample size gradually and recalculate the probability until the probability of not rejecting is less than or equal to 0.10.
**Using a Spreadsheet or Statistical Software:**
* You can use a spreadsheet program (like Excel) or statistical software (like R or Python) to efficiently calculate the hypergeometric probabilities for different sample sizes. This will help you quickly find the minimum sample size that meets the desired rejection probability.
**Example (Illustrative):**
* **n = 1:** Probability of not rejecting = (8C1) / (10C1) = 0.8
* **n = 2:** Probability of not rejecting = (8C2) / (10C2) = 0.56
* **n = 3:** Probability of not rejecting = (8C3) / (10C3) = 0.3
* **n = 4:** Probability of not rejecting = (8C4) / (10C4) = 0.1429
* **n = 5:** Probability of not rejecting = (8C5) / (10C5) = 0.051
In this example, a sample size of **n = 5** would likely satisfy the requirement, as the probability of not rejecting is less than 0.10.
**Note:**
* This is a simplified example. In real-world scenarios, you might need to consider factors like the cost of inspection, the potential consequences of rejecting a good shipment, and the desired level of consumer confidence.
* Statistical software or tables can provide more accurate and efficient calculations for the hypergeometric distribution.
I hope this helps! Let me know if you have any further questions.
Answer by ikleyn(52858)  (Show Source):
You can put this solution on YOUR website! .
A shipment of 10 items has two defective and eight non defective units.
In the inspection of the shipment, a sample of units will be selected and tested.
If a defective unit is found , the shipment of 10 units will be rejected.
If a sample of four is selected, what is the probability that the shipment will be rejected?
~~~~~~~~~~~~~~~~~~~~~~~~~~
First, the wording of the problem is  .
The correct formulation should be like THIS:
A shipment of 10 items has two defective and eight non defective units.
In the inspection of the shipment, a sample of 4 (four) units will be selected and tested.
If a defective unit is found, the shipment of 10 units will be rejected.
If a random sample of four items is tested, what is the probability that the shipment will be rejected?
Second, the flow of words and mathematical symbols in the post by @CPhill
is  to the problem.
The solution is simple, short, clear and educative.
The probability that the shipment will be rejected is equal to the probability to find at least
one defective item in the random set of 4 (four) items.
The number of all possible quadruples of 10 items is  =  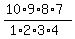= 210.
The number of all possible quadruples of the form (1 defective,3 good) is 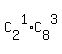 =  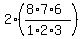= 112.
The number of all possible quadruples of the form (2 defective,2 good) is 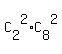 =  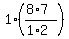= 28.
So the probability that the shipment will be rejected is
P =  =  =  . ANSWER
Solved.
/\/\/\/\/\/\/\/\/\/\/\/
The note regarding the solution by @CPhill (which is, I believe, an AI for solving math problems).
As we solve Math problems at this forum, our goal is to TEACH.
Don't spew out an insane amount of words to overwhelm the reader/(student)
with the amount of filth (sorry) as you do,
but to do something completely opposite.
COMPLETELY OPPOSITE TO what YOU do.
Now I am facing with this dilemma:
should I recommend to the owner of this site/forum
to close it from your interventions ?
////////////////////////
There are three kinds of teachers.
Best teachers are those who can teach, who love teaching and who can do it.
Bad teachers are those who can not teach, do not love teaching and can not do teaching.
But even worst teachers are those who can not teach, but, instead of it, are charged
to prove to everyone around that they " also can ".
It is the worst kind of teachers, and now your AI reminds me such teachers,
who are not able to teach, but want very much and are charged to PROVE to everyone around that they " also can ".
This idea - to prove that they " also can " - is the dominant idea and the meaning of their existence.
In my life, I saw teachers of all these kinds.
It is interesting that students are well versed in all these shades.
Naturally, students love good teachers and remember them with gratitude throughout their lives;
are neutral to the second kind of teachers and forget about them quickly;
but hate ( ! H A T E ! ) third kind of teachers, and these bad memories stay with them for a long time.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
The complement of "at least one of the four" is "none of the four".
So the probability that at least one of the four selected is defective is 1, minus the probability that none of the four is defective.
The probability that none of the four is defective is the number of ways of choosing 4 of the 8 good units, divided by the total number of ways of choosing 4 of the 10 units.
So the probability that the shipment will be rejected is 1 - 1/3 = 2/3
ANSWER: 2/3
|
|
|
