Question 1193411: The difference A-B, of two sets A and B is defined to be the set of all
elements in A that are ot in B. Use the Venn diagram to illustrate the
following sets:
(a)A − B(b)(A − B) ∩ (B − A),(c)(A ∪ B) − (A ∩ B)(c)U − A where
U denote the universal set.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Draw a rectangle to represent the universal set U
Inside the rectangle, draw partially overlapping circles labeled A and B, as shown below
===========================================================
Part (a)
The set A - B is where we shade the region inside A, but outside B. So it's the crescent shape moon highlighted in blue
Effectively set A works like the universal set and we only focus on that. Then we further reduce/shrink things down by kicking out stuff found in set B.
For more information, check out the concept of set complements.
===========================================================
Part (b)
Refer to the previous part to see how A - B is set up
Set B - A is a similar idea, but this time we shade the region marked in red
Notice how the blue and red regions do NOT have anything in common. There's no overlap.
Therefore (A − B) ∩ (B − A) will not have any shaded region and we will indicate this as an empty set.
The drawing you should submit to your teacher should look like the very first venn diagram I posted above when I didn't shade anything. Be sure to tell your teacher that the empty set is involved.
===========================================================
Part (c)
Unfortunately math tends to reuse a lot of symbols, or similarly looking symbols. The universal set U and the union symbol look very similar.
For the sake of clarity, I'll refer to the union symbol as the word "union"
So instead of writing A U B, I'll write A union B
The set A union B is the set of things inside A, B, or both sets at once.
We shade both circles and even the overlapped region between them to visually denote A union B
If we kick out the set A ∩ B, then we end up with A-B on the left and B-A on the right. We union those two pieces together to end up with (A-B) union (B-A).
In other words,
(A union B) - (A ∩ B) = (A-B) union (B-A)
The drawing is exactly the same as mentioned in part (b) when I highlighted the blue set for A-B and the red set for B-A. Though I would use one single color to indicate that we're talking about one single set. The union of A-B with B-A is almost like we're gluing the two disjointed sets together, rather than trying to see what overlapped regions they have.
===========================================================
Part (d)
The set U - A is where we start with the entire universal set U, and then kick out stuff found in A.
Therefore, we shade the region outside of A as shown below.
Be sure of course to stay inside the rectangle because we cannot get outside the universal set.
The notation U - A can be shortened to A' or 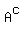 to indicate the complement of set A, or the opposite of set A.
Example:
A = set of all animals
U-A = A' = set of all things that aren't an animal
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
The difference A-B, of two sets A and B is defined to be the set of all
elements in A that are ot in B. Use the Venn diagram to illustrate the
following sets:
(a) A − B ; (b) (A − B) ∩ (B − A) ; (c) (A ∪ B) − (A ∩ B) (d) U − A where
U denote the universal set.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will give wording description for each case.
I prefer wording descriptions, because only with wording description real understanding comes.
(a) A - B is the set of all elements from A that do not belong to B.
So, A - B = A - (A ∩ B) : A - B is what remains from A when (A ∩ B) is subtracted from A. ANSWER
(b) (A − B) ∩ (B − A).
A - B is the set of elements of A that do not belong to (A ∩ B).
B - A is the set of elements of B that do not belong to (A ∩ B).
Therefore, (A − B) ∩ (B − A) is the empty set.
(c) (A ∪ B) − (A ∩ B) is the set of elements from the union of A and B, that do not belong to the intersection (A ∩ B).
In other words, (A ∪ B) − (A ∩ B) is the set of elements, that belong A_only and B_only:
we take the union of A and B and subtract the intersection (A ∩ B) from this union.
(d) U - A is the set of all elements of the universal set that do not belong to A.
The set (U - A) is called the complement set to A.
Solved : I completed my description.
Hope it helps.
|
|
|
