Question 1193384: Hi
there were 2222 participants in halls A B and C. During the first interval,3/5 in A went to B .During the second interval, 2/3 of B went over to C. During the last interval,half of C left. In the end there were twice as many participants in C as in B and twice as many participants in B as in A.
How many were in B at first.
Thanks
Found 2 solutions by greenestamps, MathTherapy:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the beginning numbers in the halls be A, B, and C.
In the first interval, 3/5 of A move to B (2/5 stay in A)
# in A: (2/5)A
# in B: B+(3/5)A
# in C: still C
In the second interval, 2/3 of those in B moved to C (1/3 remained in B)
# in A: (2/5)A
# in B: (1/3)(B+(3/5)A) = (1/3)B+(1/5)A
# in C: C+(2/3)(B+(3/5)A) = C+(2/3)B+(2/5)A
In the third interval, half of those in C left (half remained)
# in A: (2/5)A
# in B: (1/3)B+(1/5)A
# in C: (1/2)C+(1/3)B+(1/5)A
In the end, the number in B was twice the number in A:
(1/3)B+(1/5)A=2((2/5)A)
(1/3)B=(3/5)A
B=(9/5)A
And in the end, the number in C was twice the number in B:
(1/2)C+(1/3)B+(1/5)A=2((1/3)B+(1/5)A)
(1/2)C=(1/3)B+(1/5)A=(1/3)((9/5)A)+(1/5)A=(3/5)A+(1/5)A=(4/5)A
C=(8/5)A
The total number of students was 2200:
A+B+C=2200
A+(9/5)A+(8/5)A=2200
(22/5)A=2200
A=500
B=(9/5)A=900
C=(8/5)A=800
ANSWER: The number in B at the start was 900
CHECK:
start (A,B,C) = (500,900,800)
after first interval: (200,1200,800)
after second interval: (200,400,1600)
after third interval: (100,400,800)
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
there were 2222 participants in halls A B and C. During the first interval,3/5 in A went to B .During the second interval, 2/3 of B went over to C. During the last interval,half of C left. In the end there were twice as many participants in C as in B and twice as many participants in B as in A.
How many were in B at first.
Thanks
The answer from the other person is INCORRECT. It may be correct (not even going to bother to check it) for the WRONG number
he used but for a particular given number, that answer is WRONG. Read on for the correct solution and correct answer.
Let original number in A, B, and C, be A, B, and C, respectively
We then have: A + B + C = 2,222 ----- eq (i)
After  in A went to B, A had in A went to B, A had 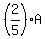 , or , or 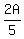 left
After left
After 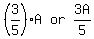 went to B, B then had: went to B, B then had: 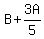 left
After left
After  of the number in B went to C, B then had of the number in B went to C, B then had  left
After left
After 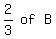 or or  or or 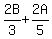 went to C, C then had: went to C, C then had:  After ½ of C left, C then had: ½ *
After ½ of C left, C then had: ½ * 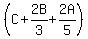 , or , or 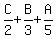 left
Since in the end, there were TWICE as many in C as in B, then, left
Since in the end, there were TWICE as many in C as in B, then,  6A + 10B - 15C = 0 ----- Multiplying by LCD, 30 ------ eq (ii)
Since in the end, there were TWICE as many in B as in A, then:
6A + 10B - 15C = 0 ----- Multiplying by LCD, 30 ------ eq (ii)
Since in the end, there were TWICE as many in B as in A, then:  9A = 5B ----- Cross-multiplying
9A = 5B ----- Cross-multiplying

 ------ Substituting ------ Substituting  for A in eq (i)
5B + 9B + 9C = 9(2,222) ---- Multiplying by LCD, 9
14B + 9C = 19,998 ------- eq (iv) for A in eq (i)
5B + 9B + 9C = 9(2,222) ---- Multiplying by LCD, 9
14B + 9C = 19,998 ------- eq (iv)
 ------ Substituting ------ Substituting  for A in eq (ii) for A in eq (ii)
 10B + 30B - 45C = 0 ------ Multiplying by LCD, 3
10B - 45C = 0
5(8B - 9C) = 5(0)
8B - 9C = 0 ------- eq (v)
22B = 19,998 ------ Adding eqs (v) & (iv)
Original number in B, or
10B + 30B - 45C = 0 ------ Multiplying by LCD, 3
10B - 45C = 0
5(8B - 9C) = 5(0)
8B - 9C = 0 ------- eq (v)
22B = 19,998 ------ Adding eqs (v) & (iv)
Original number in B, or 
|
|
|