Question 1193357: The probability that Neil studies his lesson is 3/7. The probability that he will get good grades is 1/5. What is the probability that he will get good grades given that he will study his lessons?
Found 2 solutions by danidani, ikleyn:
Answer by danidani(3)   (Show Source): (Show Source):
You can put this solution on YOUR website! The probability that Neil studies his lesson = 3/7
The probability that Neil will get good grades = 1/5
Let A=Event that Neil studies his lesson
B=Event that Neil will get good marks
The probability that he will get good grades given that he will study his lessons = ?
P(B|A)=?
P(B|A)=P(B and A)/P(A)
P(B and A)=Probability that Neil get good grades and he studies the lesson.
Here, both A and B are non Mutually Exclusive events as they have something in common. So, P(B and A)=3/7 - 1/5
P(B and A)=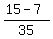
So, P(B and A)=8/35
Thus, P(B|A)=
P(B|A)=8/15
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The probability that Neil studies his lesson is 3/7. The probability that he will get good grades is 1/5.
What is the probability that he will get good grades given that he will study his lessons?
~~~~~~~~~~~~~~~~
Regarding this post, I think that the problem in the post is posed incorrectly.
To be posed correctly, the problem must provide explicitly the probability that
"Neil will get good grades if he will study his lessons."
In other words, the probability of the intersection of the two events must be given in the problem as a part of the input.
But it is missed in the post.
The assumption made by the other tutor that this probability is the difference of two other probabilities
has no any reasonable base.
So, my advise/instruction to the visitor is double check your input.
///////////////
It is a standard problem on "conditional probability",
but significant part of the problem's input is carelessly missed.
As worded, printed, posted and presented, this " problem " is DEFECTIVE.
|
|
|