Question 1193348: A soccer field has a perimeter of 288 meters and an area of 4,860 square meters. What are the dimensions of the field?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A soccer field has a perimeter of 288 meters and an area of 4,860 square meters.
What are the dimensions of the field?
~~~~~~~~~~~~~~~~~
Let x be the length, in meters; y be the width.
Then x + y = 288/2 = 144 (half of the perimeter).
Consider the arithmetic mean of x and y, which is 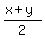 = = 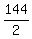 = 72.
Then, obviously, x = 72+a, y = 72-a for some value of "a" (x and y are equally remoted from the arithmetic mean).
Therefore, the area of the field is
area = x*y = (72+a)*(72-a) = = 72.
Then, obviously, x = 72+a, y = 72-a for some value of "a" (x and y are equally remoted from the arithmetic mean).
Therefore, the area of the field is
area = x*y = (72+a)*(72-a) = 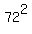 - -  = 5184 - = 5184 -  .
So, the area equation is
5184 - .
So, the area equation is
5184 -  = 4860.
From this equation, find "a" = 4860.
From this equation, find "a"
 = 5184 - 4860 = 5184 - 4860
 = 324
a = = 324
a =  = 18.
Thus the dimensions of the field are x = 72+18 = 90 meters and y = 72-18 = 54 meters.
ANSWER. The dimensions of the field are 90 meters by 54 meters. = 18.
Thus the dimensions of the field are x = 72+18 = 90 meters and y = 72-18 = 54 meters.
ANSWER. The dimensions of the field are 90 meters by 54 meters.
Solved.
The method showed in my post is non-standard method, which is rarely used in traditional school education.
Its advantage is in that in many cases it allows to get the answer without long calculations -
practically MENTALLY, as you see in the given case.
----------------
If you want to see many other similar solved problems, look into the lessons
- Problems on the area and the dimensions of a rectangle
- Three methods to find the dimensions of a rectangle when its perimeter and the area are given
in this site.
The first reference is the standard method; the second reference teaches non-standard methods.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Dimensions and the area of rectangles and circles and their elements".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|