Question 1193163: Hi
Jane gave a third of her beads and another 4 more to Sally, a third of the remaining beads and 3 more to Mary and a third of the rest plus 3 to betty.
In the end she had 3 beads left. How many did she have at first.
Thanks
Found 3 solutions by josgarithmetic, greenestamps, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the end, who? Jane?
Yes? If done the hard way, following literally and solving equation, Jane first began with 33. beads.
(You can check this and find that it works according to the description.)
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I can't imagine how the response from the other tutor would be of any use to the student, unless the student just wanted to get the answer without learning anything....
--------------------------------------------------------------------
Let's solve the problem in the "forward" direction, building an ugly-looking equation directly from the given information, and then solving that equation to find the answer to the problem.
Then we will look at how we solved that ugly equation to see how we could solve the problem faster and more easily by working "backwards".
And finally we will look at solving the problem backwards using the concept of an inverse function, which will be faster yet.
--------------------------------------------------------------------
Let x be the number of beads Jane started with.
Note that when she gives away 1/3 of the beads she has, she has 2/3 of that number of beads left; the number of beads remaining gets multiplied by 2/3.
She gave 1/3 of what she had to Sally, plus 4 more; the number she had left was 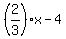
She then gave 1/3 of what she had left to Mary, plus 3 more; the number she had left was 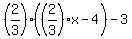
She then gave 1/3 of what she had left to Betty, plus 3 more; the number she had left was 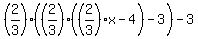
That number she had left was 3:

Solve the equation....
add 3: 
multiply by 3/2: 
add 3: 
multiply by 3/2: 
add 4: 
multiply by 3/2: 
ANSWER: Jane started with 33 beads
Now let's look at solving the problem backwards, starting with the 3 beads Jane finished with.
There are two kinds of things that happened to the number of beads Jane started with:
(1) She gave away 1/3 of what she had; leaving her with 2/3 of what she had previously. That means the number of beads she had left got multiplied by 2/3. To work backwards, we need to divide by 2/3, which means multiplying by 3/2.
(2) She gave away some number of beads; to work backwards, we need to add that number of beads.
Now work backwards, using those steps.
She finished with 3 beads.
Before that 3 was subtracted from her number of beads, so add 3 beads: 3+3=6
Before that her number of beads was multiplied by 2/3, so multiply by 3/2: 6(3/2)=9
Before that 3 was subtracted from her number of beads, so add 3: 9+3=12
Before that her number of beads was multiplied by 2/3, so multiply by 3/2: 12(3/2)=18
Before that 4 was subtracted from her number of beads, so add 4: 18+4=22
Before that her number of beads was multiplied by 2/3, so multiply by 3/2: 22(3/2)=33
Observe that the operations we performed to work backwards to get the answer are exactly the operations we performed to solve our ugly equation.
With a little practice with this kind of problem, working backwards is faster and easier for most students than writing and solving an ugly equation.
The part of the process that is hardest to understand is that (for example in this problem) when 1/3 of the beads are given away, the number remaining is multiplied by 2/3, so when working backwards at this step we need to multiply by 3/2.
Finally, for the more interested student, here is a way to do this "working backward" much more quickly.
Working backwards in a problem is like finding an inverse function. The problem tells us what happened to the original number of marbles; the final number of marbles is some function of the original number f(x). Given the final number of beads, we can find the original number using the inverse of f(x).
The function that changes the original number of marbles does the following operations:
multiply by 2/3;
subtract 4;
multiply by 2/3;
subtract 3;
multiply by 2/3,
subtract 3
The inverse function needs to perform the opposite operations, in the opposite order:
add 3;
multiply by 3/2;
add 3;
multiply by 3/2;
add 4;
multiply by 3/2
Again that sequence of operations is the same as we used in both of the previous methods for solving the problem.
Answer by MathTherapy(10553)   (Show Source): (Show Source):
|
|
|