Question 119315: Can you show me how to write the vertex form for this problem y=-0.75x^2+3x-4 and finding its x-intercepts?
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! The vertex of a parabola expressed in the form  is at the point ( , )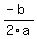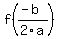
For your problem,  and  , so  and  . Therefore the vertex is at (2,-1).
The x-intercepts of a parabola are where the curve crosses the x-axis, i.e. where y = 0. To find the x-intercepts, set the function equal to 0,  and solve.
Before computing the roots of the equation using the quadratic formula, it is instructive to calculate the discriminant (the part of the quadratic formula under the radical) to determine if real roots exist for the equation.
 . Since the discriminant is negative, there are no real roots for this equation. Graphically speaking, that means that the parabola does not cross the x-axis at all, so there are no x-intercepts.
This also makes sense if you consider that the coefficient on the high order term, 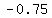 is negative indicating that the parabola is concave down and the vertex y-coordinate is also negative. Since the curve is concave down, the y-coordinate of the vertex is the maximum value the function ever achieves, meaning that the curve never takes on a positive value and therefore cannot cross the x-axis.
And here's a picture to prove it:
Hope that helps,
John
|
|
|
