Question 1193129: 5 objects, without replacement, from 18 distinct objects
If the order is relevant, how many ways can this be done?
If the order is not relevant, how many ways can this be done?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203)   (Show Source):
You can put this solution on YOUR website!
(1) If order is important, then it is a permutation.
5 objects, selected IN ORDER from 18 objects:
18 choices for the first;
17 choices for the second;
...
14 choices for the last
ANSWER: 18P5 = 18*17*16*15*14 (you can do the calculation....)
(2) If order is not important, then it is a combination.
There are 18*17*16*15*14 different orders in which you can choose 5 of the 18 objects.
Any group of 5 that you select could have been chosen in 5*4*3*2*1 different orders. So the number of distinct combinations of 5 of the 18 objects is the number of permutations, divided by the number of different orders in which those 5 objects could have been chosen.
ANSWER: 18C5 = (18*17*16*15*14)/(5*4*3*2*1) (again I leave the calculation to you)
Answer by ikleyn(52848)  (Show Source):
You can put this solution on YOUR website! .
5 objects, without replacement, from 18 distinct objects
(a) If the order is relevant, how many ways can this be done?
(b) If the order is not relevant, how many ways can this be done?
~~~~~~~~~~~~~~~
(a) If the order is relevant, then the answer is 18*17*16*15*14 = 1028160 different ways.
It is the product of 5 consecutive integer numbers in descending order, starting from 18.
It is called "permutations of the length 5 of 18 different objects".
On Permutations, see introductory lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Simple and simplest problems on permutations
- Special type permutations problems
in this site.
(b) If the order is not relevant, then the answer is
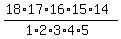 =  = 8568 different ways.
It is called "combinations of 18 different objects taken 5 at a time",
 =  .
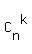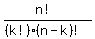On Combinations, see introductory lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
