SOLUTION: Given the hyperbola with the equation y^2 -9x^2 =-9 find the vertices, the foci, and the equations of the asymptotes.

Instead of doing your homework for you, I'll change 9 to 16
and do this one instead: 



You will do yours exactly like this, step by step:

The standard form of a hyperbola is either

 for a hyperbopla like this " )( "

or  

 for a hyperbola like this "  "

Either way, we get 1 on the right side, by dividing through by -16



Both terms on the left must have a denominator showing, so we put
1 under the second term on the left:



Reverse the terms on the left, so that the "plus" term is first:



We finish by rewriting x as (x-0) and y as (y-0)



Now that we have it in standard form, we see that it is a hyperbola
that looks like this " )( ".

Comparing it to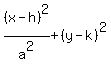 

center = (h,k) = (0,0), a2 = 1, b2 = 16, so
a = semi-transverse axis = √1 = 1 and 
b =semi-conjugate axis = √16 = 4

The defining rectangle has corners (h±a,k±b) = (0±1,0±4) or
(1,4), (-1,4), (1,-4), (-1,-4), and the asymptotes are the
extended diagonals of the defining rectangle:

    

The vertices are the ends of the transverse axis (1,0) and (-1,0),

the foci are just beyond the vertices.

To find the foci, we must find c by the Pythagorean relation for
hyperbolas:







So the foci are 

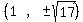I'll draw them in:


We find the equation of the asymptote that leans to the right.
It passes through the points (0,0) and (1,4).  It has slope
.

It has equation




We find the equation of the asymptote that leans to the left.
It passes through the points (0,0) and (-1,4).  It has slope
 

It has equation




Now do yours the same way, step-by-step.

Edwin