Question 1192984: A gardener has seven identical-looking tulip bulbs, of which each will produce a different color tulip. Four of the colors are unknown, however one will become white, one will become yellow, and one will become pink. She plants them abitrarily in a row. When the flowers start to bloom, what is the probability that the yellow one is first in the row, the white one is second, and the pink one is at the end of the row?
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! yellow is first with probability 1/7
white is second with probability 1/6, this order 1/42
pink is not third with 4/5
not fourth with 3/4
not fifth with 2/3
not sixth with 1/2
seventh with probability 1
so the probability of pink's being last is (1/42)(4/5)(3/4)(2/3)(1/2)=24/5040=0.00476
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
I will give another solution, which leads to the same answer.
In all, there are 7! = 7*6*5*4*3*2*1 = 5040 permutations.
Favorable are those that have 1-st yellow, 2-nd white and 7-th pink;
the rest 4 tulips may go in arbitrary order;
so the number of favorable arrangements is 4! = 24.
Therefore, the probability under the problem's question is P = 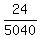 = 0.004762 (rounded). ANSWER
Solved.
|
|
|
