Question 1192919: Hi, I am confused on how to do this one.
|x-3|+4|x+2|>17
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! see my worksheet below.
see my comments below the worksheet.

the basic definition of absolute value is:
abs(x) = x, if x is positive.
abs(x) = -x, if x is negative.
by x, they mean the expression within the absolute value sign.
for example:
abs(x-3) is equal to (x-3), if the expression (x-3) is positive.
abs(x-3) is equal to -(x-3), if the expression (x-3) is negative.
so you have to break up abs(x-3) into two parts.
the first part is (x-3).
the second part is -(x-3).
that's the concept behind solving this problem.
my worksheet does that.
it breaks the problem up into:
++ ----- (x-3) + 4(x+2) > 17
-- ----- -(x-3) - 4(x+2) > 17
+- ----- (x-3) - 4(x+2) > 17
-+ ----- -(x-3) + 4(x+2) > 17
and solves each one separately.
the solutions were:
x > 2.4
x < -4.4
x < -9.3
x > 2
x > 2.4 is superfluous because it's covered by x > 2.
x - 9.3 is superfluous because it's covered by x < 4.4.
x > 2 or x < 4.4 are your solutions.
i graphed the equation of abs(x-3) + 4 * abs(x+2) = y and y = 17 to show you how that looks graphically.
that's shown below.

let me know if you have any questions.
theo
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
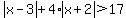
The critical points of the function on the left (where the behavior of the function changes) are at x=3 and x=-2. To solve the inequality, look for solutions on three intervals: (1) -infinity to -2; (2) -2 to 3; and (3) 3 to infinity.
(1) -infinity to -2....
On this interval, |x-3| = -x+3 and |x+2| = -x-2
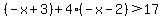
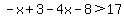
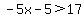
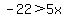
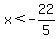
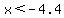
This solution is completely within the interval we are working in, so it is part of the solution to the inequality.
ANSWER (first part): Part of the solution set is the interval (-infinity,-4,4)
(2) -2 to 3....
On this interval, |x-3| = -x+3 and |x+2| = x+2
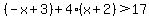
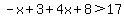
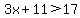
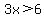

In the interval from -2 to 3, the only part that is in the solution set is x>2.
ANSWER (second part): Part of the solution set is the interval (2,3]
(3) 3 to infinity....
On this interval, |x-3| = x-3 and |x+2| = x+2
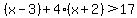
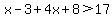
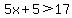
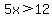
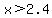
This inequality is satisfied on the entire interval we are working in, so this entire interval is part of the solution set.
ANSWER (third and last part): Part of the solution set is the interval [3,infinity).
ANSWER: The solution set of the inequality is the union of the three solution sets we found in the three intervals: (-infinity, -4.4) U (2,infinity)
A graph of the absolute value function (red) and the constant function 17 (green) shows the behavior of the absolute value function changing at x=-2 and x=3; and it shows the absolute value function being greater than 17 to the left of x=-4.4 and to the right of x=2.

|
|
|