Question 1192810: ``PROBLEM SOLVING. Analyze. Solve. Answer.
Draw diagrams wherever necessary. Round off your final answers up to 2 decimal places.
-Sara and Junya made a string telephone and tested if it works. Sara stood at the top of a tower while Junya stayed at the ground level. From Sara’s viewpoint, the angle of depression of Junya is 64° with the horizontal. Junya is 10.5 m from the base of the tower. How long is the string of their improvised telephone?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39621)   (Show Source):
Answer by ikleyn(52817)  (Show Source):
You can put this solution on YOUR website! .
Sara and Junya made a string telephone and tested if it works.
Sara stood at the top of a tower while Junya stayed at the ground level.
From Sara’s viewpoint, the angle of depression of Junya is 64° with the horizontal.
Junya is 10.5 m from the base of the tower. How long is the string of their improvised telephone?
~~~~~~~~~~~~~~~~~~~~~
The solution by @josgaritmetic is FATALLY WRONG and CONCEPTUALLY INCORRECT.
I came to bring you a correct solution.
Make a sketch.
Let x be the length of the string, in meters (the value under the problem's question).
Your sketch represents right angled triangle with the hypotenuse of x meters long.
Horizontal leg is 10.5 meters, and the angle beteen this leg and the hypotenuse
(the adjacent leg) is 64°.
So you write
x*cos(64°) = 10.5.
From this equation find x
x = 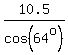 =  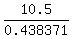= 23.95231436 meters.
We round this value to 2 decimal places to a bit greater value and get the answer 23.96 meters.
ANSWER. The length of the string is 23.96 meters, approximately.
Solved.
---------------
For the safety of your mind, ignore the post by josgarithmetic.
Keep in mind that 80% or 90% of his "solutions" at this forum are incorrect.
//////////////
After seeing my post, @josgarithmetic tried to make corrections in his post,
but his updated post is still incorrect, since he uses INCORRECT angle of 26 degrees instead of correct
depression = elevation angle of 64 degrees.
This person simply does not know elementary Math and is absolutely careless about his writing (is not able to write correctly).
|
|
|
