|
Question 1192805: A candy manufacturer makes two types of special candy, say A and B. Candy A consists of equal part dark chocolate and caramel and Candy B consists of two parts of dark chocolate and one part of walnut. The company has in stock 430 kilograms of caramel, 360 kilograms of dark chocolate and 210 kilograms of walnuts. The company sells Candy A for P285 and Candy B for P260 per kilogram. How much of each candy should the manufacturer produce to maximize profit?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A candy manufacturer makes two types of special candy, say A and B.
Candy A consists of equal part dark chocolate and caramel and
Candy B consists of two parts of dark chocolate and one part of walnut.
The company has in stock 430 kilograms of caramel, 360 kilograms of dark chocolate and 210 kilograms of walnuts.
The company sells Candy A for P285 and Candy B for P260 per kilogram.
How much of each candy should the manufacturer produce to maximize  revenue ? revenue ?
~~~~~~~~~~~~~~~~~~~
First, the question is posed incorrectly.
The correct question should ask about maximizing the revenue (not the profit).
So, I will solve the problem in this edited/modified formulation.
Let x be the amount of candy A, in kilograms;
let y be the amount of candy B.
The revenue function (the subject to maximize) is R(x,y) = 285x + 260y. (1)
The constraint inequalities are
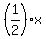 + + 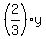 <= 360 (2) (dark chocolate) <= 360 (2) (dark chocolate)
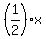 <= 430 (3) (caramel) <= 430 (3) (caramel)
 <= 210 (4) (walnuts)
x >= 0, y >= 0.
Constraints can be rewritten equivalently
3x + 4y <= 2160 (2')
x <= 860 (3')
y <= 630 (4')
The feasibility domain is shown in the plot below. <= 210 (4) (walnuts)
x >= 0, y >= 0.
Constraints can be rewritten equivalently
3x + 4y <= 2160 (2')
x <= 860 (3')
y <= 630 (4')
The feasibility domain is shown in the plot below.
 Figure. Plots 3x + 4y = 2160 (red); x = 860 (blue); y = 630 (green)
The feasibility domain is the triangle in QI, adjacent to x- and y-axis below the red line.
It is clear from the plot, that the real working constraint is (2').
The constraints (3') and (4') do not work.
In other words, the only working constraint is (2) for dark chocolate.
The other constraints (3) and (4) do not work.
+------------------------------------------------------------------------------+
| It means, that the solution and the strategy in this problem is to use |
| as much dark chocolate as possible (as constraint (2') or (2) allow it). |
+------------------------------------------------------------------------------+
Now, to get the solution in x and y variables, you have a linear function of the revenue (1)
over the triangle, which is the feasibility domain.
As the Linear Programming method says (and it is obvious from the common sense of view),
the solution is one of the two vertices of the triangle,
(x,y) = (
Figure. Plots 3x + 4y = 2160 (red); x = 860 (blue); y = 630 (green)
The feasibility domain is the triangle in QI, adjacent to x- and y-axis below the red line.
It is clear from the plot, that the real working constraint is (2').
The constraints (3') and (4') do not work.
In other words, the only working constraint is (2) for dark chocolate.
The other constraints (3) and (4) do not work.
+------------------------------------------------------------------------------+
| It means, that the solution and the strategy in this problem is to use |
| as much dark chocolate as possible (as constraint (2') or (2) allow it). |
+------------------------------------------------------------------------------+
Now, to get the solution in x and y variables, you have a linear function of the revenue (1)
over the triangle, which is the feasibility domain.
As the Linear Programming method says (and it is obvious from the common sense of view),
the solution is one of the two vertices of the triangle,
(x,y) = ( , ,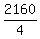 ) = (0,540) or (x,y) = ( ) = (0,540) or (x,y) = (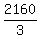 , , ) = (720,0).
So, you calculate the revenue at these two points
R(0,540) = 285*0 + 260*540 = 140400
R(720,0) = 285*720 + 260*0 = 205200.
Comparing it, you see that the optimum solution is to produce and to sell 720 kilograms of candy A and 0 kg of candy B,
which gives the maximum revenue of P205200. ANSWER ) = (720,0).
So, you calculate the revenue at these two points
R(0,540) = 285*0 + 260*540 = 140400
R(720,0) = 285*720 + 260*0 = 205200.
Comparing it, you see that the optimum solution is to produce and to sell 720 kilograms of candy A and 0 kg of candy B,
which gives the maximum revenue of P205200. ANSWER
Solved.
-------------
To see many other similar and different mini-max problems solved by the Linear Programming method, look into the lesson
- Solving minimax problems by the Linear Programming method
in this site.
|
|
|
| |