Question 1192675: Hi, I'm getting stuck, so please I need a volunteer to help me
here is the problem
For surgeries and serious injuries, anesthesiologists are responsible for administering anesthesia. If correct dosages are not given and monitored, it is possible patients may wake up during a procedure. Avoiding this disaster takes analysis of an anesthesia’s concentration in the bloodstream. When a concentration of an anesthesia is below 0.1 mg/L, it is no longer effective. In these two cases, you must use rational functions to model the anesthesia’s concentration in the bloodstream and determine when the patient may wake up.
Given a model for this patient’s concentration over time, complete the table with useful times or amounts. Use the model to determine when they may wake up. Model y =2.8x/0.4x^2+ 1.3
Fill in the table with their correct value
The first column represents the x values and the second column represents the y values
Minutes Since Dose(x) Concentration in mg/L (y)
5 → ...
10 → ...
20 → ...
30 → ...
60 → ...
... → 0.4
... → 0.2
... → 0.1
... → 0.01
1)Based on the model, when will the patient wake up?
2)If the procedure lasts approximately 1 hour and thirty minutes, will additional anesthesia be required?
3)Can you determine the maximum amount of concentration that the patient had in their bloodstream? If it is over 2 mg/L, then it could be dangerous.
Found 2 solutions by KMST, Boreal:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I asume your model function is  . .
I do not know how the problem would be solved in a nursing class,
so I am going to assume it is for an algebra, pre-calculus, or calculus class.
If you are expected to use a graphing calculator, it should not be difficult.
I am going to assume you are not expected to use a graphing calculator.
TO FIND y VALUES:
Plugging x values into that formula, I find
For  , ,  that I would round to that I would round to 
For  , I find , I find  (rounded as (rounded as  ) )
For  , I find , I find  (rounded as (rounded as  ) )
For  , I find , I find  (rounded as (rounded as  ) )
For  , I find , I find  (rounded as (rounded as  ) )
IMPORTANT NOTE:
That function should be entered into a computer program or a calculator as
y = 2.8x/(0.4x^2+ 1.3)
The parentheses are needed.
If you do not put those parentheses in the formula, it will be calculated is
  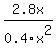  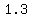 , which does not make sense for concentration in the bloodstream after one dosing. , which does not make sense for concentration in the bloodstream after one dosing.
TO FIND x VALUES:
You may be expected to "solve for x" in the formula.
Multiplying times 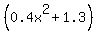 both sides of the equal sign in both sides of the equal sign in  , ,
You get  --> -->  --> -->  . .
That is a quadratic equation in  , with coefficients , with coefficients   and and  . .
Using the quadratic formula 
to solve for  , ,
we get the formula to find  as a function of as a function of  , ,
 --> --> 
Plugging the given y values into that formula, I get the following rounded values:
For  , I find , I find  . .
For  , I find , I find 
For  , I find , I find 
For  , I find , I find 
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am assuming it is y=(2.8x)/(0.4x^2+1.3).
x=5, y=14/(10+1.3)=14/11.3=1.24
x=10, y=28/41.3=0.68
x=20, y=56/161.3=0.35
x=30, y=84/361.3=0.23
x=60, y=168/1441.3=0.117
-
y=0.4=(2.8x)/(0.4x^2+1.3)
0.16x^2+0.52=2.8x
0.16x^2-2.8x+0.52=0
16x^2-280x+52=0; 4x^2-70x+13=0
x=17.3 min
-
y=0.2
0.08x^2+0.26=2.8x
0.08x^2-2.8x+0.26=0
8x^2-280x+26=0; 4x^2-140x+13=0
x=34.91 min
-
y=0.1
0.04x^2+0.13=2.8x
0.04x^-2.8x+0.13=0
4x^2-280x+13=0
x=70 min.
An hour and a half would be too long. The minimum is reached in 1h10m
-
y=0.01
0.004x^2-2.8x+0.013=0, 695 minutes
-
Substitute 2 for y
2=(2.8x)/(0.4x^2+1.3)
0.8x^2+2.6=2.8x
0.8x^2-2.8x+2.6=0
8x^2-28x+26=0
4x^2-7x+13=0, and this has complex roots, so it does not reach 2 mg/l
Take the derivative and it is y'=(0.4x^2+1.3)*2.8-(2.8x)(0.8x)/(0.4x^2+1.3)^2
set y'=0 and multiply through by the denominator, which disappears
so 1.12x^2+3.64=2.24x^2 and 1.12x^2=3.64 and x=1.80 min maximum
-
The horizontal lines are y=0.1,0.2,0.4,0.6,0.8 mg/l

|
|
|