Question 1192522: (1 point) It is estimated that approximately 8.37% Americans are afflicted with diabetes. Suppose that a certain diagnostic evaluation for diabetes will correctly diagnose 98% of all adults over 40 with diabetes as having the disease and incorrectly diagnoses 3% of all adults over 40 without diabetes as having the disease.
a) Find the probability that a randomly selected adult over 40 does not have diabetes, and is diagnosed as having diabetes (such diagnoses are called "false positives").
b) Find the probability that a randomly selected adult of 40 is diagnosed as not having diabetes.
c) Find the probability that a randomly selected adult over 40 actually has diabetes, given that he/she is diagnosed as not having diabetes (such diagnoses are called "false negatives").
(Note: it will be helpful to first draw an appropriate tree diagram modeling the situation)
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Certainly, let's break down the problem and find the probabilities.
**a) Probability of a False Positive**
* **False Positive:** This occurs when an individual *does not* have diabetes but is *incorrectly* diagnosed as having it.
* **Calculation:**
* Probability of not having diabetes: 1 - 0.0837 = 0.9163
* Probability of false positive diagnosis given no diabetes: 0.03
* Probability of false positive = 0.9163 * 0.03 = **0.0275**
**b) Probability of Being Diagnosed as Not Having Diabetes**
* **This involves two scenarios:**
* 1. **True Negative:** Individual does not have diabetes and is correctly diagnosed as not having it.
* Probability: 0.9163 (probability of not having diabetes) * 0.97 (probability of correct diagnosis given no diabetes) = 0.8895
* 2. **False Negative:** Individual has diabetes but is incorrectly diagnosed as not having it.
* Probability: 0.0837 (probability of having diabetes) * 0.02 (probability of incorrect diagnosis given diabetes) = 0.0017
* **Total Probability of Being Diagnosed as Not Having Diabetes:** 0.8895 + 0.0017 = **0.8912**
**c) Probability of False Negative**
* **False Negative:** As defined above, this is the probability of having diabetes but being incorrectly diagnosed as not having it.
* **Calculation:**
* From part (b), we calculated the probability of a false negative as 0.0017.
* To find the conditional probability of actually having diabetes given that the diagnosis is negative:
* Probability of false negative / Probability of being diagnosed as not having diabetes
* = 0.0017 / 0.8912
* = **0.0019**
**In summary:**
* a) Probability of false positive: 0.0275
* b) Probability of being diagnosed as not having diabetes: 0.8912
* c) Probability of false negative: 0.0019
**Key takeaway:** While the diagnostic test is generally accurate, there's still a small but significant risk of false positives and false negatives.
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
It is estimated that approximately 8.37% Americans are afflicted with diabetes. Suppose that a certain diagnostic evaluation for diabetes
will correctly diagnose 98% of all adults over 40 with diabetes as having the disease and incorrectly diagnoses 3% of all adults over 40
without diabetes as having the disease.
(a) Find the probability that a randomly selected adult over 40 does not have diabetes, and is diagnosed as having diabetes
(such diagnoses are called "false positives").
(b) Find the probability that a randomly selected adult  over 40 is diagnosed as not having diabetes.
(c) Find the probability that a randomly selected adult over 40 actually has diabetes, given that he/she is diagnosed as not having diabetes
(such diagnoses are called "false negatives").
~~~~~~~~~~~~~~~~
In the post by @CPhill, all three parts (a), (b) and (c) are solved and answered INCORRECTLY.
I came to bring correct solutions to all parts.
(a) In (a), they want you determine the probability of two simultaneous events:
the person does not have diabetes, but is diagnosed incorrectly as having diabetes.
The ANSWER to (a) is 0.9263*(1-0.98) = 0.018526.
(b) This probability is the sum of two probabilities of disjoint events:
- the person does not have diabetes and diagnosed correctly as not having diabetes
P1 = 0.9263*0.98;
- the person has diabetes, but diagnosed incorrectly as not having diabetes
P2 = 0.0837*0.(1-0.03).
Therefore, the probability in (b) is P = P1 + P2 = 0.9263*0.98 + 0.0837*(1-0.03) = 0.988963. ANSWER to (b)
(c) In (c), the conditional probability is
P = 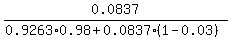 =  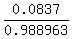= 0.084634. ANSWER to (c)
In this formula, the numerator is the probability of the event that the person has diabetes.
The denominator is the probability that he/she is diagnosed as not having diabetes.
Solved.
----------------------
The goal of this problem is to teach a student to think logically in this specific area.
Having and using common sense is enough to make every step.
Knowing the formal theorems is not required.
Referring to these formal theorems is not required, too.
It only distracts attention from the solution.
An example on how incorrectly the problem was solved in the post by @CPhill shows
that the references to formal theorems do not save from making monstrous errors.
Do not save from making monstrous errors at every step.
Common sense should work and really works much better in such simple problems.
And this is exactly my major goal in this post to help students to develop their common sense.
And it should be the major goal of every teaching on how to solve such problems.
And not at all to weave a web of references to theorems in order to demonstrate your knowledgeability.
About making errors in such problems during their solution.
I think it is normal to make 5 errors at first attempt;
3 errors at the second trial, 2 errors at the third trial,
1 error at the fourth trial and 0 (zero) errors at fifth trial.
After that, I would recommend re-solve the problem three more times
to make sure that all errors are just fixed and there are no new errors.
|
|
|
