SOLUTION: Find the equation of the tangent to; f(x) = e^-x at the point where x=2. So I know dy/dx=-1/e^x, but don't understand how I can sub that x value in the original equation and

You correctly determined the derivative function   = -.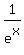


To proceed further, you should substitute x= 2 into the formula. 

Doing this way, you will find the value of the derivative at the point x= 2, which is the slope of the function

    f(x) =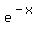 

at the point x= 2.


        So, the slope is  m = -.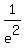


Now you know the point on the plot of the function: it is  (,) = (,);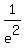

and you know the slope:  it is  m = -.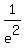


So, the equation of the tangent line is 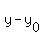  = 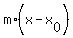,  or

    y -  = -.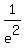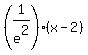


It is your ANSWER.


You can also use any other EQUIVALENT form of the last equation.