Question 1192479: The cost function for a container company is c(x)=10x+30 and the revenue function is r(x)=-x^2+24x where x is the number of containers sold in thousand. Determine the profit function for the number of containers sold. Then determine the number of containers sold that maximizes profit
I got P(x)=-x^2-8x-30 and the x would be -4 but that negative confuses me how do you sell -4 000 contains?
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The cost function for a container company is c(x)=10x+30 and the revenue function is r(x)=-x^2+24x
where x is the number of containers sold in thousand.
(a) Determine the profit function for the number of containers sold.
(a) Then determine the number of containers sold that maximizes profit
I got P(x)=-x^2-8x-30 and the x would be -4 but that negative confuses me how do you sell -4 000 contains?
~~~~~~~~~~~~~~~~~~
The formula for the profit function P(x) = -x^2 - 8x - 30, which you " got "
and to which you refer, is wrong, incorrect and absurdist.
The correct formula for the profit is
P = Revenue - Cost,
or
P(x) = (-x^2 + 24x) - (10x + 30) = -x^2 + 14x - 30.
It is the ANSWER to question (a).
To get the number of containers that maximizes the profit, use the formula
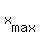 = =  ,
where "a" is the coefficient of the profit function at x^2 and b is the coefficient at x.
In your case, a= -1, b= 14; therefore ,
where "a" is the coefficient of the profit function at x^2 and b is the coefficient at x.
In your case, a= -1, b= 14; therefore
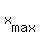 = = 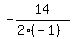 = =  = 7.
Thus the number of containers that maximizes the profit is 7 thousands.
It is the ANSWER to question (b). = 7.
Thus the number of containers that maximizes the profit is 7 thousands.
It is the ANSWER to question (b).
Solved, explained and completed.
----------------
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Learn the subject from there once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|